This page was generated from docs/Examples/Cpx_Cpx_Liq_Thermobarometry/Cpx_Liq_Thermobarometry.ipynb. Interactive online version: .

Clinopyroxene-only and Clinopyroxene-Liquid Thermobarometry.

This notebook goes through the options for clinopyroxene-Liquid thermobarometry and clinopyroxene-only thermobarometry
Cpx-Liq matching is not covered in this tutorial, there is a separate folder “Cpx_Liquid_melt_matching” for that
You can download the excel spreadsheet from: https://github.com/PennyWieser/Thermobar/blob/main/docs/Examples/Cpx_Cpx_Liq_Thermobarometry/Cpx_Liq_Example.xlsx

You need to install Thermobar once on your machine, if you haven’t done this yet, uncomment the line below (remove the #)

[1]:

#!pip install Thermobar

First, load the necessary python things

[2]:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import Thermobar as pt
pt.__version__

[2]:

'1.0.45dev'

Lets try with a different path

[3]:

from pathlib import Path
input_path = Path(r"C:\Users\penny\Box\Postdoc\MyBarometers\Thermobar_outer\docs\Examples\Cpx_Cpx_Liq_Thermobarometry")

Now, load the data - you can either have the notebook in the same folder as the spreadsheet:

[4]:

out=pt.import_excel(file_name='Cpx_Liq_Example.xlsx', sheet_name="Sheet1")
my_input=out['my_input']
Liqs=out['Liqs']
Cpxs=out['Cpxs']

Or include the path if the data is somewhere else:

[5]:

out=pt.import_excel(path=input_path, file_name='Cpx_Liq_Example.xlsx', sheet_name="Sheet1")
my_input=out['my_input']
Liqs=out['Liqs']
Cpxs=out['Cpxs']

Inspect the data to check it loaded properly

[6]:

Liqs.head()

[6]:

	SiO2_Liq	TiO2_Liq	Al2O3_Liq	FeOt_Liq	MnO_Liq	MgO_Liq	CaO_Liq	Na2O_Liq	K2O_Liq	P2O5_Liq	H2O_Liq	Sample_ID_Liq
0	51.1	0.93	17.5	8.91	0.18	6.09	11.50	3.53	0.17	0.15	3.8	0
1	51.5	1.19	19.2	8.70	0.19	4.98	10.00	3.72	0.42	0.14	6.2	1
2	59.1	0.54	19.1	5.22	0.19	3.25	7.45	4.00	0.88	0.31	6.2	2
3	52.5	0.98	19.2	8.04	0.20	4.99	9.64	4.15	0.21	0.14	6.2	3
4	56.2	0.34	20.4	5.88	0.20	2.58	7.18	6.02	1.02	0.23	6.2	4

[7]:

Cpxs.head()

[7]:

	SiO2_Cpx	TiO2_Cpx	Al2O3_Cpx	FeOt_Cpx	MnO_Cpx	MgO_Cpx	CaO_Cpx	Na2O_Cpx	Cr2O3_Cpx	Sample_ID_Cpx
0	51.5	0.50	3.70	5.18	0.09	15.8	22.8	0.24	0.66	0
1	50.3	0.73	4.12	5.83	0.00	15.0	22.7	0.24	0.28	1
2	47.3	1.75	7.85	6.51	0.14	13.1	22.5	0.25	0.22	2
3	51.1	0.63	4.41	5.66	0.13	15.6	22.6	0.23	0.27	3
4	51.0	0.56	4.14	7.33	0.20	14.4	22.4	0.31	0.09	4

Getting help

At any point, you can do help(pt.function) to get some more information
For example, here we get information on inputs/outputs for Cpx-Liq thermometry, including the equation options

[8]:

help(pt.calculate_cpx_liq_temp)

Help on function calculate_cpx_liq_temp in module Thermobar.clinopyroxene_thermobarometry:

calculate_cpx_liq_temp(*, equationT, cpx_comps=None, liq_comps=None, meltmatch=None, P=None, eq_tests=False, H2O_Liq=None, Fe3Fet_Liq=None, sigma=1, Kd_Err=0.03)
    Clinopyroxene-Liquid thermometry, calculates temperature in Kelvin
    (and equilibrium tests as an option)

    Parameters
    -------
    cpx_comps: pandas.DataFrame
        Clinopyroxene compositions with column headings SiO2_Cpx, MgO_Cpx etc.

    liq_comps: pandas.DataFrame
        Liquid compositions with column headings SiO2_Liq, MgO_Liq etc.

    Or:

    meltmatch: pandas.DataFrame
        Combined dataframe of cpx-Liquid compositions
        Used for calculate_cpx_liq_press_temp_matching function.

    EquationT: str
        Choice of equation:
        Cpx-Liquid
        |  T_Put1996_eqT1  (P-indep, H2O-indep)
        |  T_Mas2013_eqTalk1  (P-indep, H2O-indep, alk adaption of T1)
        |  T_Brug2019  (P-indep, H2O-indep)
        |  T_Put1996_eqT2 (P-dep, H2O-indep)
        |  T_Mas2013_eqTalk2  (P-dep, H2O-indep, alk adaption of T2)
        |  T_Put1999  (P-dep, H2O-indep)
        |  T_Put2003  (P-dep, H2O-indep)
        |  T_Put1999  (P-dep, H2O-indep)
        |  T_Put2008_eq33  (P-dep, H2O-dep)
        |  T_Mas2013_eqalk33  (P-dep, H2O-dep, alk adaption of eq33)
        |  T_Mas2013_Palk2012 (P-indep, H2O_dep)
        |  T_Petrelli2020_Cpx_Liq (gives voting)
        |  T_Jorgenson2022_Cpx_Liq (gives voting)
        |  T_Petrelli2020_Cpx_Liq_onnx (gives consistent result every time)


    P: float, int, pandas.Series, str  ("Solve")
        Pressure in kbar
        Only needed for P-sensitive thermometers.
        If enter P="Solve", returns a partial function
        Else, enter an integer, float, or panda series


    eq_tests: bool
        If False, just returns pressure (default) as a panda series
        If True, returns pressure, Values of Eq tests,
        Values of Eq tests (Kd, EnFs, DiHd, CaTs, CrCaTs),
        as well as user-entered cpx and liq comps and components.


    Returns
    -------
    If eq_tests=False
        pandas.Series: Temperature in Kelvin
    If eq_tests=True
        pandas.DataFrame: Temperature in Kelvin +
        Eq Tests + cpx+liq comps + components

Example 1 - Calculating Temperature

1a - Temperature for a known pressure and water content

Here, we calculate temperature using the H2O content given in the H2O_Liq column in the user-entered spreadsheet (the default), and P=5 kbar
There are a number of equations (see help above), but here we use T_Put2008_eq33 for temperature

[9]:

Temp_T33=pt.calculate_cpx_liq_temp(cpx_comps=Cpxs, liq_comps=Liqs,
                        equationT="T_Put2008_eq33", P=5)-273.15 # Default Kelvin
Temp_T33

[9]:

0     1091.562867
1     1031.605285
2      999.303442
3     1032.536881
4      979.726983
5     1076.821062
6     1096.927022
7     1097.227100
8     1113.361468
9     1084.298534
10    1091.178760
11    1071.691587
12    1089.996302
13    1028.359107
14    1028.359107
15    1028.359107
16    1093.611526
17            NaN
18    1087.546061
19    1104.700975
dtype: float64

1b - Temperature, overwriting the spreadsheet water content in the function itself

Here, we are reseting water to 0 wt%. You can see the temperatures are much higher

[10]:

Temp_T33_0H2O=pt.calculate_cpx_liq_temp(cpx_comps=Cpxs, liq_comps=Liqs,
                                        equationT="T_Put2008_eq33",
                                        P=5, H2O_Liq=0)-273.15
Temp_T33_0H2O

[10]:

0     1142.969951
1     1109.923744
2     1073.681511
3     1110.970579
4     1051.769286
5     1134.212162
6     1149.012230
7     1159.843300
8     1174.122141
9     1141.430504
10    1144.660690
11    1131.557607
12    1144.720092
13    1076.010017
14    1076.010017
15    1076.010017
16    1150.716488
17            NaN
18    1150.219143
19    1159.165100
dtype: float64

1c- Lets use the thermometer of Brugman and Till, 2019.

This returns a number of warnings, because the authors recomend a compositional calibration range, which our entered cpx compositions lie outside of.

[11]:

Temp_TBrug=pt.calculate_cpx_liq_temp(cpx_comps=Cpxs, liq_comps=Liqs,
                                    equationT="T_Brug2019", P=5)-273.15
Temp_TBrug

Youve selected a P-independent function

C:\Users\penny\AppData\Local\Temp\ipykernel_24664\1899851194.py:1: UserWarning: Some inputted CPX compositions have Cpx Mg#>0.65;.
  Temp_TBrug=pt.calculate_cpx_liq_temp(cpx_comps=Cpxs, liq_comps=Liqs,
C:\Users\penny\AppData\Local\Temp\ipykernel_24664\1899851194.py:1: UserWarning: Some inputted CPX compositions have Al2O3>7 wt%;.
  Temp_TBrug=pt.calculate_cpx_liq_temp(cpx_comps=Cpxs, liq_comps=Liqs,
C:\Users\penny\AppData\Local\Temp\ipykernel_24664\1899851194.py:1: UserWarning: Some inputted Liq compositions have  SiO2<70 wt%;
  Temp_TBrug=pt.calculate_cpx_liq_temp(cpx_comps=Cpxs, liq_comps=Liqs,
c:\users\penny\box\postdoc\mybarometers\thermobar_outer\src\Thermobar\clinopyroxene_thermobarometry.py:2213: UserWarning: which is outside the recomended calibration range of Brugman and Till (2019)
  w.warn("which is outside the recomended calibration range of Brugman and Till (2019)")

[11]:

0     1797.689417
1     1632.682392
2     1202.363348
3     1558.356437
4     1028.947694
5     1828.840169
6     1889.290499
7     1772.472552
8     1946.324399
9     1873.382098
10    1881.239956
11    1834.031996
12    1853.418730
13    1868.159678
14    1868.159678
15    1868.159678
16    1836.411331
17    1857.905516
18    1928.817708
19    1973.023872
dtype: float64

1d - We can also specify eq_tests=True to get a full dataframe back with all the components, as well as a number of equilibrium test values

You could then extract just the temps using Temp_T33_0H2O_EqTests[‘T_K_calc’] or any other column you want the same way

[12]:

Temp_T33_0H2O_EqTests=pt.calculate_cpx_liq_temp(cpx_comps=Cpxs, liq_comps=Liqs,
                                                equationT="T_Put2008_eq33",
                                                P=5, H2O_Liq=0, eq_tests=True)
Temp_T33_0H2O_EqTests

Using Fe3FeT from input file to calculate Kd Fe-Mg

[12]:

	P_kbar_calc	T_K_calc	Eq Tests Neave2017?	Delta_Kd_Put2008	Delta_Kd_Mas2013	Delta_EnFs_Mollo13	Delta_EnFs_Put1999	Delta_CaTs_Put1999	Delta_DiHd_Mollo13	Delta_DiHd_Put1999	...	Delta_EnFs_I_M_Mollo13	CaTs_Pred_Put1999	Delta_CaTs_I_M_Put1999	CrCaTs_Pred_Put1999	Delta_CrCaTs_I_M_Put1999	CaTi_Pred_Put1999	Delta_CaTi_I_M_Put1999	Jd_Pred_Put1999	Delta_Jd_Put1999	Delta_Jd_I_M_Put1999
0	5	1416.119951	False	0.042816	0.094027	0.010858	0.021183	0.016957	0.089424	0.001586	...	-0.010858	0.013418	-0.016957	0.000000	0.009562	0.043320	0.002307	0.016184	0.000872	0.000872
1	5	1383.073744	False	0.036792	0.090778	0.007575	0.021866	0.023796	0.104285	0.024207	...	-0.007575	0.013021	-0.023796	0.000000	0.004122	0.056932	0.011994	0.017429	0.000099	0.000099
2	5	1346.831511	False	0.058659	0.172858	0.043395	0.013382	0.075254	0.006413	0.103915	...	0.043395	0.016630	-0.075254	0.000000	0.003245	0.029418	0.042249	0.018331	0.000246	0.000246
3	5	1384.120579	False	0.034331	0.101144	0.012488	0.028698	0.031526	0.084045	0.024697	...	-0.012488	0.014301	-0.031526	0.000000	0.003909	0.050962	0.009764	0.019332	0.002997	0.002997
4	5	1324.919286	False	0.022156	0.097447	0.021106	0.049019	0.032121	0.071950	0.035481	...	-0.021106	0.010990	-0.032121	0.000000	0.001315	0.050713	0.014761	0.027953	0.005738	0.005738
5	5	1407.362162	False	0.011745	0.133688	0.008645	0.029286	0.012999	0.062059	0.001463	...	-0.008645	0.012999	0.012999	0.297720	0.277125	0.057369	0.026926	0.019470	0.006126	0.006126
6	5	1422.162230	False	0.011959	0.091270	0.008903	0.024363	0.014640	0.070686	0.003636	...	-0.008903	0.014640	0.014640	0.130559	0.110135	0.052890	0.032902	0.015664	0.002722	0.002722
7	5	1432.993300	False	0.052296	0.077646	0.007652	0.024590	0.015888	0.054068	0.010131	...	-0.007652	0.015888	0.015888	0.148010	0.125617	0.045423	0.029060	0.018272	0.011840	0.011840
8	5	1447.272141	False	0.046595	0.085580	0.020659	0.043637	0.007563	0.082456	0.039311	...	-0.020659	0.016662	0.007563	0.001101	0.017485	0.052715	0.016339	0.015821	0.008622	0.008622
9	5	1414.580504	False	0.018097	0.116199	0.015372	0.032515	0.013343	0.083869	0.008159	...	-0.015372	0.013343	0.013343	0.003516	0.010965	0.059753	0.014958	0.018210	0.004591	0.004591
10	5	1417.810690	True	0.015009	0.141280	0.004910	0.020402	0.014748	0.058127	0.012136	...	-0.004910	0.014748	0.014748	0.857156	0.836370	0.043707	0.041545	0.016472	0.003230	0.003230
11	5	1404.707607	True	0.015558	0.109274	0.013261	0.021390	0.015494	0.050272	0.041881	...	-0.013261	0.015494	0.015494	0.001648	0.014651	0.047981	0.032592	0.017360	0.009224	0.009224
12	5	1417.870092	False	0.044544	0.063790	0.019190	0.035825	0.014555	0.060011	0.001347	...	-0.019190	0.014555	0.014555	0.574581	0.555774	0.052013	0.036050	0.016889	0.002411	0.002411
13	5	1349.160017	True	0.014011	0.133748	0.047904	0.041739	0.012404	0.016132	0.150795	...	-0.047904	0.012404	0.012404	0.052732	0.042651	0.054363	0.026279	0.019044	0.018319	0.018319
14	5	1349.160017	True	0.014011	0.133748	0.047904	0.041739	0.012404	0.016132	0.150795	...	-0.047904	0.012404	0.012404	0.052732	0.042651	0.054363	0.026279	0.019044	0.018319	0.018319
15	5	1349.160017	True	0.014011	0.133748	0.047904	0.041739	0.012404	0.016132	0.150795	...	-0.047904	0.012404	0.012404	0.052732	0.042651	0.054363	0.026279	0.019044	0.018319	0.018319
16	5	1423.866488	True	0.002518	0.111409	0.013153	0.031786	0.015716	0.050165	0.001366	...	-0.013153	0.015716	0.015716	0.356916	0.342040	0.052646	0.035059	0.018291	0.002126	0.002126
17	5	NaN	False	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	0.603117	0.588110	NaN	NaN	NaN	NaN	NaN
18	5	1423.369143	False	0.006558	0.108254	0.012578	0.032440	0.014620	0.067687	0.009856	...	-0.012578	0.014620	0.014620	0.160617	0.141226	0.060201	0.021519	0.017590	0.003868	0.003868
19	5	1432.315100	False	0.007279	0.123765	0.011986	0.036870	0.014680	0.077193	0.026064	...	-0.011986	0.014680	0.014680	0.310037	0.296888	0.056968	0.030100	0.016562	0.002476	0.002476

20 rows × 130 columns

Example 2 - Calculating pressure for a known temperature

2a - Pressure at fixed temperature (T=1300 K), and pressures from Neave and Putirka (2017)

[13]:

P_FixedTNeave=pt.calculate_cpx_liq_press(cpx_comps=Cpxs, liq_comps=Liqs,
                                       equationP="P_Neave2017", T=1300)
P_FixedTNeave

[13]:

0      0.634602
1      1.655874
2      1.146083
3      1.028349
4      3.854147
5      0.077818
6      0.103202
7      3.902001
8      3.198764
9     -0.172497
10    -0.067569
11    -2.437195
12     0.531826
13   -14.887115
14   -14.887115
15   -14.887115
16     1.346623
17          NaN
18     0.405712
19     1.682571
dtype: float64

2b - Equation 30 from Putirka (2008), overwriting input water, return equilibrium tests

Here we change equation P, overwrite the H2O content in the function, and ask for equilibrium tests.
We are selecting equation 30 from Putirka (2008) this time, T=1300 K

[14]:

Temp_P30_0H2O=pt.calculate_cpx_liq_press(cpx_comps=Cpxs, liq_comps=Liqs,
                                         equationP="P_Put2008_eq30",
                                         T=1300, H2O_Liq=0, eq_tests=True)
Temp_P30_0H2O

Using Fe3FeT from input file to calculate Kd Fe-Mg

[14]:

	P_kbar_calc	T_K_calc	Eq Tests Neave2017?	Delta_Kd_Put2008	Delta_Kd_Mas2013	Delta_EnFs_Mollo13	Delta_EnFs_Put1999	Delta_CaTs_Put1999	Delta_DiHd_Mollo13	Delta_DiHd_Put1999	...	Delta_EnFs_I_M_Mollo13	CaTs_Pred_Put1999	Delta_CaTs_I_M_Put1999	CrCaTs_Pred_Put1999	Delta_CrCaTs_I_M_Put1999	CaTi_Pred_Put1999	Delta_CaTi_I_M_Put1999	Jd_Pred_Put1999	Delta_Jd_Put1999	Delta_Jd_I_M_Put1999
0	-2.090909	1300	False	0.015390	0.116829	0.002696	0.003912	0.019173	0.089851	0.350659	...	-0.002696	0.011202	-0.019173	0.000000	0.009562	0.047180	0.006167	0.016165	0.000891	0.000891
1	-2.604072	1300	True	0.016996	0.108121	0.006605	0.005373	0.025431	0.049622	0.286210	...	0.006605	0.011385	-0.025431	0.000000	0.004122	0.060657	0.015718	0.017407	0.000077	0.000077
2	-2.145841	1300	False	0.069927	0.183575	0.074576	0.029940	0.076260	0.125978	0.249574	...	0.074576	0.015625	-0.076260	0.000000	0.003245	0.030292	0.041375	0.018308	0.000223	0.000223
3	-2.334004	1300	False	0.014291	0.117657	0.003134	0.008701	0.033245	0.066274	0.281808	...	0.003134	0.012582	-0.033245	0.000000	0.003909	0.054136	0.012939	0.019308	0.002973	0.002973
4	-0.177987	1300	False	0.016126	0.102892	0.007476	0.045035	0.032562	0.004383	0.113023	...	-0.007476	0.010549	-0.032562	0.000000	0.001315	0.051697	0.015744	0.027927	0.005712	0.005712
5	-3.656248	1300	False	0.037163	0.157156	0.008999	0.005334	0.011085	0.129807	0.319319	...	0.008999	0.011085	0.011085	0.297720	0.277125	0.061850	0.022445	0.019441	0.006098	0.006098
6	-3.959117	1300	False	0.016846	0.121449	0.007682	0.004097	0.012259	0.135041	0.353721	...	0.007682	0.012259	0.012259	0.130559	0.110135	0.057515	0.028277	0.015640	0.002698	0.002698
7	0.216684	1300	False	0.021028	0.105244	0.007877	0.010227	0.013249	0.108774	0.364703	...	-0.007877	0.013249	0.013249	0.148010	0.125617	0.049502	0.024980	0.018258	0.011854	0.011854
8	-0.678349	1300	False	0.012104	0.115746	0.019128	0.005116	0.004551	0.094621	0.357156	...	-0.019128	0.013650	0.004551	0.001101	0.017485	0.057933	0.011121	0.015807	0.008636	0.008636
9	-3.118628	1300	False	0.008977	0.139129	0.002217	0.008054	0.011220	0.104703	0.331041	...	-0.002217	0.011220	0.011220	0.003516	0.010965	0.064853	0.009859	0.018185	0.004566	0.004566
10	-3.748095	1300	False	0.042821	0.166301	0.012878	0.009837	0.012445	0.143123	0.361588	...	0.012878	0.012445	0.012445	0.857156	0.836370	0.047356	0.037895	0.016447	0.003205	0.003205
11	-5.694960	1300	False	0.009248	0.131688	0.014536	0.006415	0.013332	0.163945	0.361704	...	0.014536	0.013332	0.013332	0.001648	0.014651	0.051503	0.029071	0.017328	0.009192	0.009192
12	-3.317520	1300	False	0.016718	0.092009	0.002553	0.004621	0.012336	0.131747	0.336589	...	-0.002553	0.012336	0.012336	0.574581	0.555774	0.056241	0.031822	0.016866	0.002388	0.002388
13	-15.728385	1300	False	0.025832	0.144548	0.038085	0.028394	0.011485	0.292357	0.321371	...	0.038085	0.011485	0.011485	0.052732	0.042651	0.056334	0.024309	0.018975	0.018250	0.018250
14	-15.728385	1300	False	0.025832	0.144548	0.038085	0.028394	0.011485	0.292357	0.321371	...	0.038085	0.011485	0.011485	0.052732	0.042651	0.056334	0.024309	0.018975	0.018250	0.018250
15	-15.728385	1300	False	0.025832	0.144548	0.038085	0.028394	0.011485	0.292357	0.321371	...	0.038085	0.011485	0.011485	0.052732	0.042651	0.056334	0.024309	0.018975	0.018250	0.018250
16	-2.753658	1300	False	0.026676	0.140028	0.000281	0.000271	0.013269	0.140658	0.350210	...	0.000281	0.013269	0.013269	0.356916	0.342040	0.057028	0.030677	0.018268	0.002102	0.002102
17	NaN	1300	False	0.000180	0.108710	NaN	0.014766	NaN	NaN	0.316925	...	NaN	NaN	NaN	0.603117	0.588110	0.058863	0.028817	NaN	NaN	NaN
18	-3.583424	1300	False	0.022523	0.136594	0.003481	0.002846	0.012271	0.132330	0.343415	...	0.003481	0.012271	0.012271	0.160617	0.141226	0.065393	0.016327	0.017565	0.003843	0.003843
19	-1.870615	1300	False	0.023835	0.151004	0.003511	0.002818	0.012196	0.105839	0.342393	...	-0.003511	0.012196	0.012196	0.310037	0.296888	0.062186	0.024882	0.016543	0.002495	0.002495

20 rows × 130 columns

2c - As above, but setting a fixed Fe3Fet_Liq ratio

Can overwrite the Fe3Fet in the input spreadsheet to a different value, affects calculations of delta Kd as this uses just Fe2+ in the melt
Note, it is debated whether Kd Fe-Mg should be calculated with all Fe (to do that here, specify Fe3Fet_Liq=0, Putirka), or using just Fe2+ (e.g., Neave and Putirka, 2017)
you can compare the delta Kd Put 2008 in this option from the answers above. You can see, by adding 30% Fe3+, you have become further from equilibrium

[15]:

Temp_P30_0H2O_30Fe=pt.calculate_cpx_liq_press(cpx_comps=Cpxs,
                    liq_comps=Liqs, equationP="P_Put2008_eq30",
                    T=1300, H2O_Liq=0, Fe3Fet_Liq=0.3, eq_tests=True)
Temp_P30_0H2O_30Fe

[15]:

	P_kbar_calc	T_K_calc	Eq Tests Neave2017?	Delta_Kd_Put2008	Delta_Kd_Mas2013	Delta_EnFs_Mollo13	Delta_EnFs_Put1999	Delta_CaTs_Put1999	Delta_DiHd_Mollo13	Delta_DiHd_Put1999	...	Delta_EnFs_I_M_Mollo13	CaTs_Pred_Put1999	Delta_CaTs_I_M_Put1999	CrCaTs_Pred_Put1999	Delta_CrCaTs_I_M_Put1999	CaTi_Pred_Put1999	Delta_CaTi_I_M_Put1999	Jd_Pred_Put1999	Delta_Jd_Put1999	Delta_Jd_I_M_Put1999
0	-2.090909	1300	False	0.080646	0.212865	0.002696	0.003912	0.019173	0.089851	0.350659	...	-0.002696	0.011202	-0.019173	0.000000	0.009562	0.047180	0.006167	0.016165	0.000891	0.000891
1	-2.604072	1300	False	0.078351	0.203468	0.006605	0.005373	0.025431	0.049622	0.286210	...	0.006605	0.011385	-0.025431	0.000000	0.004122	0.060657	0.015718	0.017407	0.000077	0.000077
2	-2.145841	1300	False	0.202528	0.316176	0.074576	0.029940	0.076260	0.125978	0.249574	...	0.074576	0.015625	-0.076260	0.000000	0.003245	0.030292	0.041375	0.018308	0.000223	0.000223
3	-2.334004	1300	False	0.082216	0.214165	0.003134	0.008701	0.033245	0.066274	0.281808	...	0.003134	0.012582	-0.033245	0.000000	0.003909	0.054136	0.012939	0.019308	0.002973	0.002973
4	-0.177987	1300	False	0.079595	0.198613	0.007476	0.045035	0.032562	0.004383	0.113023	...	-0.007476	0.010549	-0.032562	0.000000	0.001315	0.051697	0.015744	0.027927	0.005712	0.005712
5	-3.656248	1300	False	0.155721	0.275715	0.008999	0.005334	0.011085	0.129807	0.319319	...	0.008999	0.011085	0.011085	0.297720	0.277125	0.061850	0.022445	0.019441	0.006098	0.006098
6	-3.959117	1300	False	0.126698	0.231301	0.007682	0.004097	0.012259	0.135041	0.353721	...	0.007682	0.012259	0.012259	0.130559	0.110135	0.057515	0.028277	0.015640	0.002698	0.002698
7	0.216684	1300	False	0.072592	0.198864	0.007877	0.010227	0.013249	0.108774	0.364703	...	-0.007877	0.013249	0.013249	0.148010	0.125617	0.049502	0.024980	0.018258	0.011854	0.011854
8	-0.678349	1300	False	0.085341	0.213191	0.019128	0.005116	0.004551	0.094621	0.357156	...	-0.019128	0.013650	0.004551	0.001101	0.017485	0.057933	0.011121	0.015807	0.008636	0.008636
9	-3.118628	1300	False	0.115456	0.245608	0.002217	0.008054	0.011220	0.104703	0.331041	...	-0.002217	0.011220	0.011220	0.003516	0.010965	0.064853	0.009859	0.018185	0.004566	0.004566
10	-3.748095	1300	False	0.163805	0.287285	0.012878	0.009837	0.012445	0.143123	0.361588	...	0.012878	0.012445	0.012445	0.857156	0.836370	0.047356	0.037895	0.016447	0.003205	0.003205
11	-5.694960	1300	False	0.115844	0.238283	0.014536	0.006415	0.013332	0.163945	0.361704	...	0.014536	0.013332	0.013332	0.001648	0.014651	0.051503	0.029071	0.017328	0.009192	0.009192
12	-3.317520	1300	False	0.078749	0.187476	0.002553	0.004621	0.012336	0.131747	0.336589	...	-0.002553	0.012336	0.012336	0.574581	0.555774	0.056241	0.031822	0.016866	0.002388	0.002388
13	-15.728385	1300	False	0.139535	0.258251	0.038085	0.028394	0.011485	0.292357	0.321371	...	0.038085	0.011485	0.011485	0.052732	0.042651	0.056334	0.024309	0.018975	0.018250	0.018250
14	-15.728385	1300	False	0.139535	0.258251	0.038085	0.028394	0.011485	0.292357	0.321371	...	0.038085	0.011485	0.011485	0.052732	0.042651	0.056334	0.024309	0.018975	0.018250	0.018250
15	-15.728385	1300	False	0.139535	0.258251	0.038085	0.028394	0.011485	0.292357	0.321371	...	0.038085	0.011485	0.011485	0.052732	0.042651	0.056334	0.024309	0.018975	0.018250	0.018250
16	-2.753658	1300	False	0.140741	0.254093	0.000281	0.000271	0.013269	0.140658	0.350210	...	0.000281	0.013269	0.013269	0.356916	0.342040	0.057028	0.030677	0.018268	0.002102	0.002102
17	NaN	1300	False	0.102375	0.211265	NaN	0.014766	NaN	NaN	0.316925	...	NaN	NaN	NaN	0.603117	0.588110	0.058863	0.028817	NaN	NaN	NaN
18	-3.583424	1300	False	0.134808	0.248879	0.003481	0.002846	0.012271	0.132330	0.343415	...	0.003481	0.012271	0.012271	0.160617	0.141226	0.065393	0.016327	0.017565	0.003843	0.003843
19	-1.870615	1300	False	0.136682	0.263851	0.003511	0.002818	0.012196	0.105839	0.342393	...	-0.003511	0.012196	0.012196	0.310037	0.296888	0.062186	0.024882	0.016543	0.002495	0.002495

20 rows × 130 columns

Example 3 - Iterating pressure and temperature

In reality, unlesa you are an experimentalist, you rarely know one of pressure or temperature
In Keith Putirka’s spreadsheets, you can link up columns to iterate P and T towards a solution, this can be done here using the function calculate_cpx_liq_press_temp…

3a - Iterating equation 30 from Putirka (2008) for P, and equation 33 from Putirka (2008) for T

Without specifying anything else, you get a dataframe with columns for calculated pressure and temperature

[16]:

PT_iter_30_31=pt.calculate_cpx_liq_press_temp(cpx_comps=Cpxs, liq_comps=Liqs,
                                              equationP="P_Put2008_eq30",
                                              equationT="T_Put2008_eq33")
PT_iter_30_31

[16]:

	P_kbar_calc	T_K_calc	Delta_P_kbar_Iter	Delta_T_K_Iter
0	2.530914	1352.408784	0.0	0.0
1	1.786845	1290.151507	0.0	0.0
2	1.171520	1255.933868	0.0	0.0
3	2.143416	1292.669093	0.0	0.0
4	2.763538	1243.469600	0.0	0.0
5	0.535148	1328.353392	0.0	0.0
6	0.493360	1347.611001	0.0	0.0
7	6.377576	1377.397773	0.0	0.0
8	5.742168	1390.374437	0.0	0.0
9	1.396263	1339.752950	0.0	0.0
10	0.644651	1342.785453	0.0	0.0
11	-1.883972	1312.045437	0.0	0.0
12	1.211110	1344.398677	0.0	0.0
13	-14.685454	1217.300913	0.0	0.0
14	-14.685454	1217.300913	0.0	0.0
15	-14.685454	1217.300913	0.0	0.0
16	2.168816	1352.629530	0.0	0.0
17	NaN	NaN	NaN	NaN
18	1.315338	1342.522331	0.0	0.0
19	3.494361	1370.176239	0.0	0.0

3b - Same as above, but with eq_tests=True

Get all equilibrium tests, and input compostions as a larger dataframe.

[17]:

PT_iter_30_31_EqTests=pt.calculate_cpx_liq_press_temp(cpx_comps=Cpxs, liq_comps=Liqs, equationP="P_Put2008_eq30",
                                                      equationT="T_Put2008_eq33", eq_tests=True)
PT_iter_30_31_EqTests

Using Fe3FeT from input file to calculate Kd Fe-Mg

[17]:

	P_kbar_calc	T_K_calc	Eq Tests Neave2017?	Delta_P_kbar_Iter	Delta_T_K_Iter	Delta_Kd_Put2008	Delta_Kd_Mas2013	Delta_EnFs_Mollo13	Delta_EnFs_Put1999	Delta_CaTs_Put1999	...	Delta_EnFs_I_M_Mollo13	CaTs_Pred_Put1999	Delta_CaTs_I_M_Put1999	CrCaTs_Pred_Put1999	Delta_CrCaTs_I_M_Put1999	CaTi_Pred_Put1999	Delta_CaTi_I_M_Put1999	Jd_Pred_Put1999	Delta_Jd_Put1999	Delta_Jd_I_M_Put1999
0	2.530914	1352.408784	True	0.0	0.0	0.027981	0.106599	0.011304	0.009468	0.018174	...	-0.011304	0.012201	-0.018174	0.000000	0.009562	0.045314	0.004301	0.016178	0.000878	0.000878
1	1.786845	1290.151507	True	0.0	0.0	0.014591	0.110154	0.009917	0.002832	0.025619	...	-0.009917	0.011198	-0.025619	0.000000	0.004122	0.061147	0.016209	0.017420	0.000090	0.000090
2	1.171520	1255.933868	False	0.0	0.0	0.080784	0.193537	0.046615	0.050574	0.077199	...	0.046615	0.014686	-0.077199	0.000000	0.003245	0.031201	0.040466	0.018319	0.000234	0.000234
3	2.143416	1292.669093	False	0.0	0.0	0.012502	0.119081	0.015465	0.006444	0.033388	...	-0.015465	0.012439	-0.033388	0.000000	0.003909	0.054443	0.013245	0.019323	0.002988	0.002988
4	2.763538	1243.469600	False	0.0	0.0	0.002154	0.115101	0.025085	0.033393	0.033542	...	-0.025085	0.009568	-0.033542	0.000000	0.001315	0.054153	0.018201	0.027943	0.005728	0.005728
5	0.535148	1328.353392	False	0.0	0.0	0.030307	0.151008	0.003629	0.013160	0.011592	...	-0.003629	0.011592	0.011592	0.297720	0.277125	0.060562	0.023733	0.019456	0.006112	0.006112
6	0.493360	1347.611001	True	0.0	0.0	0.005393	0.109769	0.003040	0.009391	0.013188	...	-0.003040	0.013188	0.013188	0.130559	0.110135	0.055566	0.030226	0.015652	0.002710	0.002710
7	6.377576	1377.397773	False	0.0	0.0	0.039499	0.089259	0.019500	0.013119	0.014794	...	-0.019500	0.014794	0.014794	0.148010	0.125617	0.046990	0.027492	0.018277	0.011835	0.011835
8	5.742168	1390.374437	False	0.0	0.0	0.033597	0.097318	0.031008	0.032361	0.006409	...	-0.031008	0.015508	0.006409	0.001101	0.017485	0.054544	0.014511	0.015824	0.008619	0.008619
9	1.396263	1339.752950	True	0.0	0.0	0.000606	0.131231	0.013266	0.018402	0.011957	...	-0.013266	0.011957	0.011957	0.003516	0.010965	0.062936	0.011776	0.018199	0.004581	0.004581
10	0.644651	1342.785453	False	0.0	0.0	0.032515	0.157280	0.000830	0.003555	0.013284	...	0.000830	0.013284	0.013284	0.857156	0.836370	0.045922	0.039329	0.016460	0.003218	0.003218
11	-1.883972	1312.045437	False	0.0	0.0	0.006324	0.129135	0.000306	0.002289	0.013585	...	-0.000306	0.013585	0.013585	0.001648	0.014651	0.051055	0.029518	0.017340	0.009204	0.009204
12	1.211110	1344.398677	True	0.0	0.0	0.027407	0.081454	0.015105	0.018898	0.013175	...	-0.015105	0.013175	0.013175	0.574581	0.555774	0.054522	0.033541	0.016879	0.002401	0.002401
13	-14.685454	1217.300913	False	0.0	0.0	0.046407	0.162372	0.017760	0.005585	0.009986	...	0.017760	0.009986	0.009986	0.052732	0.042651	0.060200	0.020443	0.018975	0.018250	0.018250
14	-14.685454	1217.300913	False	0.0	0.0	0.046407	0.162372	0.017760	0.005585	0.009986	...	0.017760	0.009986	0.009986	0.052732	0.042651	0.060200	0.020443	0.018975	0.018250	0.018250
15	-14.685454	1217.300913	False	0.0	0.0	0.046407	0.162372	0.017760	0.005585	0.009986	...	0.017760	0.009986	0.009986	0.052732	0.042651	0.060200	0.020443	0.018975	0.018250	0.018250
16	2.168816	1352.629530	True	0.0	0.0	0.014033	0.127948	0.012246	0.016146	0.014315	...	-0.012246	0.014315	0.014315	0.356916	0.342040	0.055025	0.032680	0.018283	0.002118	0.002118
17	NaN	NaN	False	NaN	NaN	NaN	NaN	NaN	NaN	NaN	...	NaN	NaN	NaN	0.603117	0.588110	NaN	NaN	NaN	NaN	NaN
18	1.315338	1342.522331	True	0.0	0.0	0.012280	0.126901	0.010194	0.015470	0.013084	...	-0.010194	0.013084	0.013084	0.160617	0.141226	0.063446	0.018274	0.017580	0.003858	0.003858
19	3.494361	1370.176239	True	0.0	0.0	0.007055	0.136635	0.015152	0.023994	0.013518	...	-0.015152	0.013518	0.013518	0.310037	0.296888	0.059237	0.027832	0.016558	0.002479	0.002479

20 rows × 132 columns

Example 3 - Cpx-only Barometry

Very similar to above, just don’t need liq_comps input

3a -Pressure only, using equation 32b (at T=1300 K), and H2O=0

This equation requires H2O content in the liquid. If you don’t enter anything, it assumes H2O=0
else specify using H2O_Liq=….
it prints a warning telling you that by defualt, this is what the function is doing

[18]:

eq32b_noH=pt.calculate_cpx_only_press(cpx_comps=Cpxs, T=1300,
       equationP="P_Put2008_eq32b")
eq32b_noH

c:\users\penny\box\postdoc\mybarometers\thermobar_outer\src\Thermobar\clinopyroxene_thermobarometry.py:3293: UserWarning: This Cpx-only barometer is sensitive to H2O content of the liquid.  By default, this function uses H2O=0 wt%, else you can enter a value of H2O_Liq in the function
  w.warn('This Cpx-only barometer is sensitive to H2O content of the liquid. '

[18]:

0     -1.567381
1     -1.202221
2     -0.317946
3     -0.996608
4      0.467437
5     -6.911370
6     -6.286860
7    -11.586143
8     -3.498491
9    -13.658623
10   -11.540359
11   -13.391546
12   -14.272181
13   -18.202136
14   -18.202136
15   -18.202136
16   -10.918332
17          NaN
18    -5.618846
19    -8.241059
dtype: float64

3b - Pressure only, using 5 wt% water

[19]:

eq32b_5H=pt.calculate_cpx_only_press(cpx_comps=Cpxs, T=1300,
       equationP="P_Put2008_eq32b", H2O_Liq=5)
eq32b_5H

[19]:

0      0.697619
1      1.062779
2      1.947054
3      1.268392
4      2.732437
5     -4.646370
6     -4.021860
7     -9.321143
8     -1.233491
9    -11.393623
10    -9.275359
11   -11.126546
12   -12.007181
13   -15.937136
14   -15.937136
15   -15.937136
16    -8.653332
17          NaN
18    -3.353846
19    -5.976059
dtype: float64

3c - Temperature-only using eq 32d at 5 kbar

[20]:

eq32d_5kbar=pt.calculate_cpx_only_temp(cpx_comps=Cpxs, equationT="T_Put2008_eq32d",
         P=5)
eq32d_5kbar

[20]:

0     1457.849197
1     1441.107847
2     1415.899813
3     1455.722443
4     1441.512524
5     1413.510042
6     1420.741893
7     1406.196227
8     1463.728870
9     1393.605045
10    1239.894412
11    1413.752159
12    1402.402180
13    1360.089648
14    1360.089648
15    1360.089648
16    1366.264788
17    1381.658652
18    1396.089868
19    1412.298889
dtype: float64

3d - Iterating P from 32b, and T from 32d, with H2O=5

[21]:

eq32b_32d_5H=pt.calculate_cpx_only_press_temp(cpx_comps=Cpxs, equationT="T_Put2008_eq32d",
       equationP="P_Put2008_eq32b", H2O_Liq=5)
eq32b_32d_5H

[21]:

	P_kbar_calc	T_K_calc	Delta_P_kbar_Iter	Delta_T_K_Iter	SiO2_Cpx	TiO2_Cpx	Al2O3_Cpx	FeOt_Cpx	MnO_Cpx	MgO_Cpx	...	Jd	Jd_from 0=Na, 1=Al	CaTs	CaTi	DiHd_1996	EnFs	DiHd_2003	Di_Cpx	FeIII_Wang21	FeII_Wang21
0	3.889323	1448.656494	0.000000e+00	0.000000e+00	51.500000	0.500000	3.700000	5.180000	0.090000	15.800000	...	0.017055	0	0.030375	0.041013	0.814436	0.103827	0.814436	0.686042	0.035332	0.123446
1	3.721484	1430.647515	0.000000e+00	0.000000e+00	50.300000	0.730000	4.120000	5.830000	0.000000	15.000000	...	0.017330	0	0.036817	0.044938	0.819939	0.097220	0.819939	0.673165	0.040732	0.140847
2	3.982623	1407.721620	0.000000e+00	0.000000e+00	47.300000	1.750000	7.850000	6.510000	0.140000	13.100000	...	0.018085	0	0.091885	0.071667	0.732671	0.099545	0.732671	0.570239	0.038619	0.164508
3	4.567865	1452.151021	2.273737e-13	1.818989e-12	51.100000	0.630000	4.410000	5.660000	0.130000	15.600000	...	0.016335	0	0.045827	0.041197	0.796049	0.114596	0.796049	0.658834	0.039859	0.133524
4	5.941303	1449.216073	0.000000e+00	0.000000e+00	51.000000	0.560000	4.140000	7.330000	0.200000	14.400000	...	0.022215	0	0.043110	0.035953	0.806694	0.106652	0.806694	0.623678	0.038138	0.188429
5	-4.055503	1340.840204	2.273737e-13	1.591616e-12	51.893554	0.985648	4.374039	6.014774	0.427037	15.882719	...	0.013343	1	0.000000	0.084295	0.792618	0.110258	0.792618	0.645602	0.105585	0.071935
6	-3.177367	1354.783292	0.000000e+00	0.000000e+00	51.671503	1.222254	4.424609	5.755014	0.537483	15.849673	...	0.012942	1	0.000000	0.085792	0.788624	0.108885	0.788624	0.644849	0.091360	0.078945
7	-9.419020	1291.083222	0.000000e+00	0.000000e+00	52.462671	0.861366	4.306456	5.521574	0.093405	15.931721	...	0.030112	1	0.000000	0.074483	0.768475	0.116216	0.768475	0.641596	0.085759	0.077164
8	1.553018	1435.084291	0.000000e+00	0.000000e+00	52.341465	0.558521	4.332519	5.307290	0.531408	16.743678	...	0.024443	0	0.009099	0.069054	0.768797	0.135942	0.768797	0.642889	0.071195	0.085917
9	-11.734771	1261.200708	-2.273737e-13	-1.591616e-12	51.905733	0.643097	3.880163	5.651830	0.614606	16.146415	...	0.013619	1	0.000000	0.074712	0.802701	0.111995	0.802701	0.659037	0.116120	0.052394
10	-9.147761	1140.304548	0.000000e+00	0.000000e+00	51.705545	0.697444	4.406196	5.746137	0.443832	15.907585	...	0.013242	1	0.000000	0.085252	0.784209	0.112455	0.784209	0.643591	0.159222	0.010809
11	-11.304233	1282.889304	0.000000e+00	0.000000e+00	52.200291	1.467759	4.077400	5.607369	0.832626	16.045590	...	0.008136	1	0.000000	0.080574	0.778118	0.114853	0.778118	0.634926	0.082786	0.082406
12	-12.328411	1264.435549	0.000000e+00	0.000000e+00	51.725315	0.745761	4.586485	5.736715	0.550561	16.407623	...	0.014478	1	0.000000	0.088062	0.774008	0.128816	0.774008	0.636936	0.130621	0.038544
13	-16.327464	1195.406373	0.000000e+00	0.000000e+00	51.892711	0.918335	3.879493	6.001785	0.224476	16.766705	...	0.000724	1	0.000000	0.080643	0.789095	0.137203	0.789095	0.653001	0.167476	0.010370
14	-16.327464	1195.406373	0.000000e+00	0.000000e+00	51.892711	0.918335	3.879493	6.001785	0.224476	16.766705	...	0.000724	1	0.000000	0.080643	0.789095	0.137203	0.789095	0.653001	0.167476	0.010370
15	-16.327464	1195.406373	0.000000e+00	0.000000e+00	51.892711	0.918335	3.879493	6.001785	0.224476	16.766705	...	0.000724	1	0.000000	0.080643	0.789095	0.137203	0.789095	0.653001	0.167476	0.010370
16	-9.015029	1257.554261	0.000000e+00	0.000000e+00	52.006582	1.490563	4.633149	6.150716	0.383969	15.823193	...	0.016166	1	0.000000	0.087705	0.765280	0.121381	0.765280	0.621245	0.130527	0.049936
17	NaN	NaN	NaN	NaN	51.986059	1.119548	4.107258	5.587534	0.869447	16.661904	...	0.000000	1	0.000000	0.087680	0.785434	0.125194	0.785434	0.644977	0.159251	0.004758
18	-2.884479	1333.597198	0.000000e+00	0.000000e+00	52.066983	1.070126	4.261572	5.845278	0.276057	16.038723	...	0.013722	1	0.000000	0.081720	0.779896	0.117953	0.779896	0.642299	0.131180	0.041246
19	-5.607345	1327.248553	2.273737e-13	1.818989e-12	51.973899	0.809677	4.665615	5.864718	0.840250	16.467894	...	0.019037	1	0.000000	0.087068	0.777534	0.128604	0.777534	0.632774	0.145446	0.026854

20 rows × 49 columns

Example 4 - Plotting a Cpx-Liq Rhodes diagram to assess Fe-Mg equilibrium using fixed Kd values

The function calculate_cpx_rhodes_diagram_lines calculates the lines needed for the plot in a number of ways
There is disagrement in the literature as to whether Kd Fe-Mg should be assessed using just Fe2+ in the melt, or FeT, so we show both scenarios here.

Step 1 - Calculate Mg# for liq and cpxs

A number of functions in thermobar let you do it, we use this one here because it returns Mg#s for both phases

[22]:

cpx_comps_Fe3=pt.calculate_clinopyroxene_liquid_components(liq_comps=Liqs,
                cpx_comps=Cpxs, Fe3Fet_Liq=0.2)

Mgnos of Cpx are stored in the column accesed by cpx_comps_Fe3[‘Mgno_Cpx’]
Mgnos of Liq are stored in the column accesed by cpx_comps_Fe3[‘Mgno_Liq_noFe3’], for no Fe3, or cpx_comps_Fe3[‘Mgno_Liq_Fe2’] using just Fe2+ (e.g., 20% of Fe is 3+ here)

Step 2 - Calculate equilibrium lines to show on the rhodes diagram

You tell the function the min and max glass Mg# you want to show, e.g., the xspan of your plot
It returns lines for Kd=0.28+-0.08 after Putirka (2008)

[23]:

# Want to calculate Mg# to show on diagram between say 0.4 and 0.7 for the glass
eq_lines_1=pt.calculate_cpx_rhodes_diagram_lines(Min_Mgno=0.4, Max_Mgno=0.7)
eq_lines_1

[23]:

	Mg#_Liq	Eq_Cpx_Mg# (Kd=0.28)	Eq_Cpx_Mg# (Kd=0.2)	Eq_Cpx_Mg# (Kd=0.36)
0	0.400000	0.704225	0.769231	0.649351
1	0.403030	0.706845	0.771462	0.652217
2	0.406061	0.709445	0.773672	0.655065
3	0.409091	0.712025	0.775862	0.657895
4	0.412121	0.714586	0.778032	0.660707
...	...	...	...	...
95	0.687879	0.887273	0.916801	0.859588
96	0.690909	0.888681	0.917874	0.861287
97	0.693939	0.890081	0.918941	0.862979
98	0.696970	0.891473	0.920000	0.864662
99	0.700000	0.892857	0.921053	0.866337

100 rows × 4 columns

Step 3 - Combine these on a plot

You might need to adust the x and y limits of this plot for your own data

[24]:

fig, (ax1) = plt.subplots(1, 1, figsize = (6,5))
ax1.plot(eq_lines_1['Mg#_Liq'], eq_lines_1['Eq_Cpx_Mg# (Kd=0.2)'], ':r', label="K$_d$=0.2")
ax1.plot(eq_lines_1['Mg#_Liq'], eq_lines_1['Eq_Cpx_Mg# (Kd=0.36)'], ':r', label="K$_d$=0.36")
ax1.plot(eq_lines_1['Mg#_Liq'], eq_lines_1['Eq_Cpx_Mg# (Kd=0.28)'], '-r', label="K$_d$=0.28")

ax1.plot(cpx_comps_Fe3['Mgno_Liq_noFe3'], cpx_comps_Fe3['Mgno_Cpx'], '*k', mfc='yellow', ms=8, label="No Fe3")
ax1.plot(cpx_comps_Fe3['Mgno_Liq_Fe2'], cpx_comps_Fe3['Mgno_Cpx'], 'dk', mfc='green', ms=8, label="20% Fe3")
ax1.legend()
ax1.set_xlabel('Mg# Glass')
ax1.set_ylabel('Mg# Cpx')
# adjust x and y limits
ax1.set_xlim([0.4, 0.7])
ax1.set_ylim([0.6, 0.95])

[24]:

(0.6, 0.95)

../../_images/Examples_Cpx_Cpx_Liq_Thermobarometry_Cpx_Liq_Thermobarometry_53_1.png

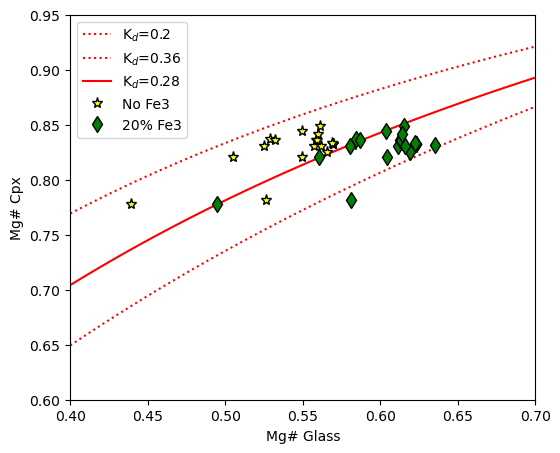
Example 5 - Rhodes diagram using equation 35 of Putirka to calculate Kd as a function of T.

Here, we plot the equilibrium fields on the Rhodes diagram using equation 35 of Putirka, which is T-sensitive
Must specify T in Kelvin. Then return column for default 0.28, as well as the results for Putirka eq 35.

[25]:

eq_lines_2=pt.calculate_cpx_rhodes_diagram_lines(Min_Mgno=0.4, Max_Mgno=0.7, T=1300)
eq_lines_2.head()

[25]:

	Mg#_Liq	Eq_Cpx_Mg# (Kd=0.28)	Eq_Cpx_Mg# (Kd=0.2)	Eq_Cpx_Mg# (Kd=0.36)	Kd_Eq35_P2008	Eq_Cpx_Mg# (Kd from Eq 35 P2008)	Eq_Cpx_Mg# (Eq 35 P2008)+0.08	Eq_Cpx_Mg# (Eq 35 P2008)-0.08
0	0.400000	0.704225	0.769231	0.649351	0.239475	0.735720	0.676036	0.806964
1	0.403030	0.706845	0.771462	0.652217	0.239475	0.738165	0.678791	0.808921
2	0.406061	0.709445	0.773672	0.655065	0.239475	0.740589	0.681528	0.810858
3	0.409091	0.712025	0.775862	0.657895	0.239475	0.742993	0.684246	0.812775
4	0.412121	0.714586	0.778032	0.660707	0.239475	0.745377	0.686945	0.814673

[26]:

fig, (ax1) = plt.subplots(1, 1, figsize = (6,5))
ax1.plot(eq_lines_2['Mg#_Liq'], eq_lines_2['Eq_Cpx_Mg# (Kd from Eq 35 P2008)'], '-r', label="K$_d$=Put eq 35")
ax1.plot(eq_lines_2['Mg#_Liq'], eq_lines_2['Eq_Cpx_Mg# (Eq 35 P2008)+0.08'], ':r', label="K$_d$=Put eq 35 + 0.08")
ax1.plot(eq_lines_2['Mg#_Liq'], eq_lines_2['Eq_Cpx_Mg# (Eq 35 P2008)-0.08'], ':r', label="K$_d$=Put eq 35 - 0.08")
ax1.set_xlim([0.4, 0.7])
ax1.plot(cpx_comps_Fe3['Mgno_Liq_noFe3'], cpx_comps_Fe3['Mgno_Cpx'], '*k', mfc='yellow', ms=8, label="No Fe3")
ax1.plot(cpx_comps_Fe3['Mgno_Liq_Fe2'], cpx_comps_Fe3['Mgno_Cpx'], 'dk', mfc='green', ms=8, label="20% Fe3")
ax1.legend()
ax1.set_xlabel('Mg# Glass')
ax1.set_ylabel('Mg# Cpx')

# adjust x and y limits
ax1.set_xlim([0.4, 0.7])
ax1.set_ylim([0.6, 0.95])

[26]:

(0.6, 0.95)

../../_images/Examples_Cpx_Cpx_Liq_Thermobarometry_Cpx_Liq_Thermobarometry_56_1.png

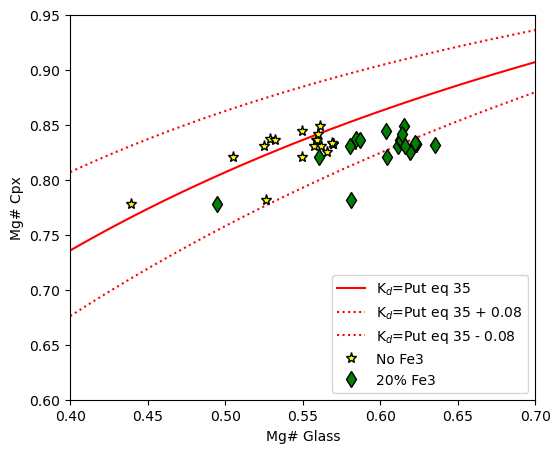
Example 6 - You can also specify a minimum and maximum Kd value you wish to calculate Rhodes lines for (here 0.2, 0.3)

[27]:

eq_lines_3=pt.calculate_cpx_rhodes_diagram_lines(Min_Mgno=0.4, Max_Mgno=0.7, KdMin=0.2, KdMax=0.3)
eq_lines_3.head()

[27]:

	Mg#_Liq	Eq_Cpx_Mg# (Kd=0.28)	Eq_Cpx_Mg# (Kd=0.2)	Eq_Cpx_Mg# (Kd=0.36)	Eq_Cpx_Mg# (KdMin=0.2)	Eq_Cpx_Mg# (KdMax=0.3)
0	0.400000	0.704225	0.769231	0.649351	0.769231	0.689655
1	0.403030	0.706845	0.771462	0.652217	0.771462	0.692348
2	0.406061	0.709445	0.773672	0.655065	0.773672	0.695021
3	0.409091	0.712025	0.775862	0.657895	0.775862	0.697674
4	0.412121	0.714586	0.778032	0.660707	0.778032	0.700309

[28]:

fig, (ax1) = plt.subplots(1, 1, figsize = (6,5))
ax1.plot(eq_lines_3['Mg#_Liq'], eq_lines_3['Eq_Cpx_Mg# (KdMin=0.2)'], ':r', label="K$_d$=Put eq 35 + 0.08")
ax1.plot(eq_lines_3['Mg#_Liq'], eq_lines_3['Eq_Cpx_Mg# (KdMax=0.3)'], ':r', label="K$_d$=Put eq 35 - 0.08")
ax1.set_xlim([0.4, 0.7])
ax1.plot(cpx_comps_Fe3['Mgno_Liq_noFe3'], cpx_comps_Fe3['Mgno_Cpx'], '*k', mfc='yellow', ms=8, label="No Fe3")
ax1.plot(cpx_comps_Fe3['Mgno_Liq_Fe2'], cpx_comps_Fe3['Mgno_Cpx'], 'dk', mfc='green', ms=8, label="20% Fe3")
ax1.legend()
ax1.set_xlabel('Mg# Glass')
ax1.set_ylabel('Mg# Cpx')

# adjust x and y limits
ax1.set_xlim([0.4, 0.7])
ax1.set_ylim([0.6, 0.95])

[28]:

(0.6, 0.95)

../../_images/Examples_Cpx_Cpx_Liq_Thermobarometry_Cpx_Liq_Thermobarometry_59_1.png

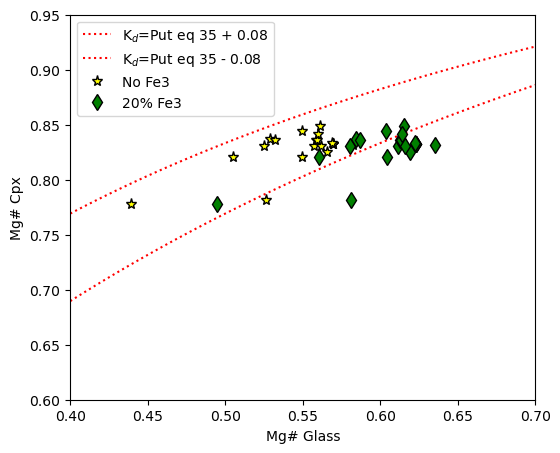
Example 7 - Can get all options by specifying a temp, and a min and max Kd

Can then plot them however you want.

[29]:

eq_lines_4=pt.calculate_cpx_rhodes_diagram_lines(Min_Mgno=0.4, Max_Mgno=0.7, T=1300, KdMin=0.2, KdMax=0.3)
eq_lines_4.head()

[29]:

	Mg#_Liq	Eq_Cpx_Mg# (Kd=0.28)	Eq_Cpx_Mg# (Kd=0.2)	Eq_Cpx_Mg# (Kd=0.36)	Kd_Eq35_P2008	Eq_Cpx_Mg# (Kd from Eq 35 P2008)	Eq_Cpx_Mg# (Eq 35 P2008)+0.08	Eq_Cpx_Mg# (Eq 35 P2008)-0.08	Eq_Cpx_Mg# (KdMin=0.2)	Eq_Cpx_Mg# (KdMax=0.3)
0	0.400000	0.704225	0.769231	0.649351	0.239475	0.735720	0.676036	0.806964	0.769231	0.689655
1	0.403030	0.706845	0.771462	0.652217	0.239475	0.738165	0.678791	0.808921	0.771462	0.692348
2	0.406061	0.709445	0.773672	0.655065	0.239475	0.740589	0.681528	0.810858	0.773672	0.695021
3	0.409091	0.712025	0.775862	0.657895	0.239475	0.742993	0.684246	0.812775	0.775862	0.697674
4	0.412121	0.714586	0.778032	0.660707	0.239475	0.745377	0.686945	0.814673	0.778032	0.700309

Calcs with all possible equations

[30]:

# If you want to run calcs with the machine learning expressions,
# you need to install this extra package. Else, this will work fine without and just not give those answers

[31]:

# uncomment this line if you havent installed already!
#!pip install "https://github.com/PennyWieser/Thermobar_onnx/archive/refs/tags/v.0.0.4.zip"

[32]:

all_pt_cpx_liq=pt.calculate_cpx_liq_press_all_eqs(liq_comps=Liqs,
                cpx_comps=Cpxs)
all_pt_cpx_liq.head()

We have reset the index on Cpx and Liq comps for the Petrelli expressions
Youve selected a P-independent function
Youve selected a T-independent function
Youve selected a T-independent function
Im normalizing using the Jorgenson method, e.g. 100 total, 2dp
Im normalizing using the Jorgenson method, e.g. 100 total, 2dp
Youve selected a P-independent function
Youve selected a T-independent function
Youve selected a T-independent function

[32]:

	P_kbar: (P_Neave17, T_Put2008_eq33)	T_K: (P_Neave17, T_Put2008_eq33)	P_kbar: (P_Neave17, T_Put2008_eq34_cpx_sat)	T_K: (P_Neave17, T_Put2008_eq34_cpx_sat)	P_kbar: (P_Put2008_eq30, T_Put2008_eq33)	T_K: (P_Put2008_eq30, T_Put2008_eq33)	P_kbar: (P_Put2008_eq31, T_Put2008_eq33)	T_K: (P_Put2008_eq31, T_Put2008_eq33)	P_kbar: (P_Put2008_eq32c, T_Put2008_eq33)	T_K: (P_Put2008_eq32c, T_Put2008_eq33)	...	P_kbar: (P_Put2008_eq32c, T_Put2008_eq34)	T_K: (P_Put2008_eq32c, T_Put2008_eq34))	P_kbar: (P2003 P&T)	T_K: (P2003 P&T)	T_K: (P_Put1996_eqP1, T_Put1996_eqT2)	P_kbar: (P_Put1996_eqP1, T_Put1996_eqT2)	P_kbar: (Petrelli, 2020)	T_K: (Petrelli, 2020)	P_kbar: (Jorgenson, 2022)	T_K: (Jorgenson, 2022)
0	0.960631	1344.698427	1.161345	1372.216226	2.530914	1352.408784	2.386186	1351.694450	2.209868	1350.825212	...	4.653251	1402.264846	0.947885	1429.684711	1431.212441	2.587626	2.329420	1365.986364	1.0	1355.15
1	1.583720	1289.239285	1.816406	1323.941135	1.786845	1290.151507	2.624094	1293.925217	1.870946	1290.529579	...	4.453012	1344.888862	0.453851	1388.379217	1410.593746	1.759554	2.445954	1282.522727	2.0	1285.15
2	0.895589	1254.759806	1.055286	1283.601656	1.171520	1255.933868	5.162310	1273.163405	6.281137	1278.078913	...	9.615150	1348.268665	-0.946284	1362.151670	1402.050070	0.278452	2.000000	1238.150000	2.0	1238.15
3	0.952699	1287.319189	1.130722	1317.160073	2.143416	1292.669093	2.225915	1293.041408	2.332966	1293.524848	...	4.859417	1346.713288	-0.021555	1387.134284	1408.805156	1.263705	2.000000	1273.150000	2.0	1273.15
4	3.581562	1246.894077	3.771286	1283.856794	2.763538	1243.469600	2.113770	1240.762861	1.456253	1238.035814	...	3.559098	1282.306231	-1.003005	1307.655434	1373.636951	1.791782	2.000000	1238.150000	2.0	1238.15

5 rows × 26 columns

[33]:

all_pt_cpx_only=pt.calculate_cpx_only_press_all_eqs(
                cpx_comps=Cpxs)
all_pt_cpx_only.head()

[33]:

	P_Wang21_eq1	T_Wang21_eq2	T_Jorgenson22	P_Jorgenson22	T_Petrelli20	T_Put_Teq32d_Peq32a	T_Put_Teq32d_Peq32b	P_Petrelli20	P_Put_Teq32d_Peq32a	P_Put_Teq32d_Peq32b	...	EnFs	DiHd_2003	Di_Cpx	FeIII_Wang21	FeII_Wang21	H2O_Liq	T_Put_Teq32d_subsol_Peq32a	T_Put_Teq32d_subsol_Peq32b	P_Put_Teq32d_subsol_Peq32a	P_Put_Teq32d_subsol_Peq32b
0	1.171230	1440.358697	1355.152954	1.000001	1342.737793	1429.010995	1423.934424	2.002911	1.515722	0.902362	...	0.103827	0.814436	0.686042	0.035332	0.123446	None	1147.861295	1083.173193	7.038781	-0.307139
1	0.500630	1429.224347	1285.151611	2.000002	1332.734375	1413.354443	1406.830074	2.376496	1.607834	0.810392	...	0.097220	0.819939	0.673165	0.040732	0.140847	None	1126.101733	1056.468462	8.994531	0.813312
2	0.882985	1373.014871	1238.150146	2.000002	1238.154541	1416.604337	1385.069856	2.000006	5.087644	1.164715	...	0.099545	0.732671	0.570239	0.038619	0.164508	None	1131.385058	1047.494247	12.020262	1.985596
3	1.452333	1433.283620	1273.152954	2.000002	1273.150513	1436.877879	1427.367498	2.000006	2.719843	1.569105	...	0.114596	0.796049	0.658834	0.039859	0.133524	None	1164.764522	1100.925908	6.984321	-0.156942
4	1.986290	1418.418850	1238.150146	2.000002	1238.154541	1427.089374	1424.835650	2.000006	3.237622	2.962238	...	0.106652	0.806694	0.623678	0.038138	0.188429	None	1155.385488	1095.094118	8.306445	1.438251

5 rows × 60 columns