This page was generated from docs/Examples/Error_propagation/Cpx_only_contour_plot.ipynb. Interactive online version: .

Python Notebook Download

Error propagation - Cpx-only

• This notebook gives a worked example showing how to propagate uncertainty for Cpx-only thermometry for different amounts of EPMA-based error on Na\(_2\)O measurements.

• We use the functionality provided by Pyrolite to contour the results from Monte Carlo simulations, as well as hexplot.

• If you use the pyroplot.density command, please remember to cite Pyrolite! (Williams et al., (2020). pyrolite: Python for geochemistry. Journal of Open Source Software, 5(50), 2314, doi: 10.21105/joss.02314)

• This builds on from the notebook showing how to consider error in a single phase (Liquid_Thermometry_error_prop.ipynb). We suggest you look at that first, as its simpler when you don’t have to worry about two separate phases

• We consider an example Cpx composition from Gleeson et al. (2020) - https://doi.org/10.1093/petrology/egaa094

• You can download the Excel spreadsheet here: https://github.com/PennyWieser/Thermobar/blob/main/docs/Examples/Error_propagation/Gleeson2020_Cpx_Comps.xlsx

You need to install Thermobar once on your machine, if you haven’t done this yet, uncomment the line below (remove the #)

#!pip install Thermobar

You will also need to install pyrolite for this example, if you haven’t done so already, uncomment the line below

#!pip install pyrolite

# Import other python stuff
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import Thermobar as pt
import sympy as sym
pd.options.display.max_columns = None
import pyrolite

Importing data

• Note, we haven’t bothered to add the “_Cpx” names after each oxide, so we simply use “suffix=”_Cpx” when we load the data

out=pt.import_excel('Gleeson2020_Cpx_Comps.xlsx', sheet_name="Sheet1", suffix="_Cpx")
my_input=out['my_input']
myCpxs1=out['Cpxs']

Lets select 1 Cpx to run the calculations on

• The [[ ]] keeps it as a dataframe

myCpxs1.iloc[[0]]

	SiO2_Cpx	TiO2_Cpx	Al2O3_Cpx	FeOt_Cpx	MnO_Cpx	MgO_Cpx	CaO_Cpx	Na2O_Cpx	K2O_Cpx	Cr2O3_Cpx	Sample_ID_Cpx
0	51.3863	0.467	4.1961	3.8654	0.12	16.3137	21.3039	0.378	0.0007	1.0191	0

Work out errors

• The Cameca software used to analyse these Cpxs returns the error as absolute elemental wt%, ignoring Oxygen, for each element (helpful!). These are loaded in as Na_Err, Si_Err….

• This means that you need to do some steps to work out the analytical error on each Cpx. We show these steps below.

• First, we decide it easiest to use the convert_oxide_percent_to_element_weight_percent function to convert measured Cpx compositions as oxides into wt% to compare to these errors. Without oxygen = True, does the calculations without oxygen. You can use this function for any phase, just specify what suffix your phase has.

Cpx_conv=pt.convert_oxide_percent_to_element_weight_percent(df=myCpxs1, suffix='_Cpx', without_oxygen=True)
Cpx_conv.head()

	Si_wt_noO2	Mg_wt_noO2	Fe_wt_noO2	Ca_wt_noO2	Al_wt_noO2	Na_wt_noO2	K_wt_noO2	Mn_wt_noO2	Ti_wt_noO2	Cr_wt_noO2	P_wt_noO2	F_wt_noO2	H_wt_noO2	Cl_wt_noO2
0	43.155184	17.675115	5.398069	27.354400	3.989980	0.503819	0.001044	0.166972	0.502666	1.252750	0.0	0.0	0.0	0.0
1	42.432683	17.004438	5.468846	27.558497	4.967044	0.507369	0.000447	0.121440	0.625890	1.313346	0.0	0.0	0.0	0.0
2	42.399838	16.694183	5.608834	27.398388	5.209677	0.523472	0.022141	0.141541	0.681296	1.320631	0.0	0.0	0.0	0.0
3	42.649103	17.224819	5.638033	27.496627	4.631102	0.538772	0.004336	0.097927	0.632681	1.086601	0.0	0.0	0.0	0.0
4	41.057438	15.479289	7.324030	26.604851	6.874709	0.702197	0.025343	0.188588	1.005908	0.737648	0.0	0.0	0.0	0.0

• Now we calculate the % error for each element. For example, for Na, we take the Cameca error (column Na_Err), and compare it to the concentration we just calculated in wt% for Na (column Na_wt_noO2 in the Cpx_conv dataframe)

Perc_Err_Na=100*my_input['Na_Err']/Cpx_conv['Na_wt_noO2']
Perc_Err_Na.head()

0    8.534819
1    8.553938
2    8.520041
3    8.315210
4    7.049307
dtype: float64

# We now need to re-arrange these into a form that we can load into the function.
# We make a new dataframe of these errors
df_Cpx_Err=pd.DataFrame(data={'SiO2_Cpx_Err': 100*my_input['Si_Err']/Cpx_conv['Si_wt_noO2'],
                            'TiO2_Cpx_Err':100*my_input['Ti_Err']/Cpx_conv['Ti_wt_noO2'],
                             'Al2O3_Cpx_Err':100*my_input['Al_Err']/Cpx_conv['Al_wt_noO2'],
                             'FeOt_Cpx_Err':100*my_input['Fe_Err']/Cpx_conv['Fe_wt_noO2'],
                            'MnO_Cpx_Err':100*my_input['Mn_Err']/Cpx_conv['Mn_wt_noO2'],
                            'MgO_Cpx_Err':100*my_input['Mg_Err']/Cpx_conv['Mg_wt_noO2'],
                            'CaO_Cpx_Err':100*my_input['Ca_Err']/Cpx_conv['Ca_wt_noO2'],
                            'Na2O_Cpx_Err':100*my_input['Na_Err']/Cpx_conv['Na_wt_noO2'],
                            'Cr2O3_Cpx_Err':100*my_input['Cr_Err']/Cpx_conv['Cr_wt_noO2'],
                               'K2O_Cpx_Err': 100*my_input['K_Err']/Cpx_conv['K_wt_noO2']}, index=[0])

Lets select 1 Cpx, and its corresponding error as an example

• using [[ ]] keeps it as a dataframe, we reset the index because sometimes this can cause python mayhem.

Cpx_1=myCpxs1.iloc[[0]].reset_index(drop=True)
Cpx_1_Err=df_Cpx_Err.iloc[[0]].reset_index(drop=True)
Cpx_1_Err

	SiO2_Cpx_Err	TiO2_Cpx_Err	Al2O3_Cpx_Err	FeOt_Cpx_Err	MnO_Cpx_Err	MgO_Cpx_Err	CaO_Cpx_Err	Na2O_Cpx_Err	Cr2O3_Cpx_Err	K2O_Cpx_Err
0	1.186416	2.148544	0.907273	3.056648	27.309951	1.129271	0.858363	8.534819	5.172622	1934.77739

Lets calculate the errors for this Cpx

• You could do this for all Cpxs, rather than just this 1 sample, but it’ll take longer, so we do a cut down version here!

• 20,000 iterations may seem like a lot, but it really helps with the contouring

Calc_Cpx_dist=pt.add_noise_sample_1phase(phase_comp=Cpx_1, phase_err=Cpx_1_Err,
                                            phase_err_type="Perc", duplicates=20000, err_dist="normal")

All negative numbers replaced with zeros. If you wish to keep these, set positive=False

Lets calculate pressures and temperatures using a wide variety of equations for Cpx-only thermobarometry

• This cell takes abit of time, its 20,000 calculations using a wide variety of P and T equations!

Calc_PT=pt.calculate_cpx_only_press_all_eqs(cpx_comps=Calc_Cpx_dist)
Calc_PT.head()

	P_Wang21_eq1	T_Wang21_eq2	T_Jorgenson22	P_Jorgenson22	T_Petrelli20	T_Put_Teq32d_Peq32a	T_Put_Teq32d_Peq32b	P_Petrelli20	P_Put_Teq32d_Peq32a	P_Put_Teq32d_Peq32b	Jd_from 0=Na, 1=Al	SiO2_Cpx	TiO2_Cpx	Al2O3_Cpx	FeOt_Cpx	MnO_Cpx	MgO_Cpx	CaO_Cpx	Na2O_Cpx	K2O_Cpx	Cr2O3_Cpx	Sample_ID_Cpx_Num	Sample_ID_Cpx	Si_Cpx_cat_6ox	Mg_Cpx_cat_6ox	Fet_Cpx_cat_6ox	Ca_Cpx_cat_6ox	Al_Cpx_cat_6ox	Na_Cpx_cat_6ox	K_Cpx_cat_6ox	Mn_Cpx_cat_6ox	Ti_Cpx_cat_6ox	Cr_Cpx_cat_6ox	oxy_renorm_factor	Al_IV_cat_6ox	Al_VI_cat_6ox	En_Simple_MgFeCa_Cpx	Fs_Simple_MgFeCa_Cpx	Wo_Simple_MgFeCa_Cpx	Cation_Sum_Cpx	Ca_CaMgFe	Lindley_Fe3_Cpx	Lindley_Fe2_Cpx	Lindley_Fe3_Cpx_prop	CrCaTs	a_cpx_En	Mgno_Cpx	Jd	CaTs	CaTi	DiHd_1996	EnFs	DiHd_2003	Di_Cpx	FeIII_Wang21	FeII_Wang21	H2O_Liq	T_Put_Teq32d_subsol_Peq32a	T_Put_Teq32d_subsol_Peq32b	P_Put_Teq32d_subsol_Peq32a	P_Put_Teq32d_subsol_Peq32b
0	5.298283	1495.270546	1462.955933	6.266479	1433.501587	1499.862431	1490.210316	3.676231	6.457578	5.314680	0	51.434957	0.472438	4.174971	3.801613	0.130219	16.309334	21.147857	0.349307	0.000000	0.976087	0.0	0	1.896576	0.896513	0.117229	0.835510	0.181435	0.024973	0.000000	0.004067	0.013103	0.028455	0.0	0.103424	0.078012	0.484798	0.063393	0.451809	3.997862	0.451809	0.000000	0.117229	0.000000	0.014227	0.123134	0.884357	0.024973	0.053039	0.025192	0.743051	0.135346	0.743051	0.654499	-0.004277	0.121506	0	1242.728053	1196.499937	5.135329	0.357257
1	5.653239	1501.279659	1450.841553	6.104247	1442.768066	1503.368823	1494.296353	3.903188	6.959813	5.885026	0	51.547228	0.470622	4.213829	3.918778	0.082694	16.210466	21.097138	0.386442	0.000000	1.035990	0.0	0	1.897759	0.889692	0.120654	0.832209	0.182839	0.027585	0.000000	0.002579	0.013033	0.030154	0.0	0.102241	0.080598	0.482858	0.065482	0.451660	3.996504	0.451660	0.000000	0.120654	0.000000	0.015077	0.123341	0.880578	0.027585	0.053014	0.024614	0.739505	0.135421	0.739505	0.649536	-0.006992	0.127646	0	1245.302199	1200.315002	5.417295	0.766908
2	5.264089	1484.098940	1442.657593	7.011894	1437.181274	1485.307199	1472.272972	4.864007	5.893007	4.339467	0	50.638955	0.485152	4.216327	3.795194	0.174312	16.213989	21.452416	0.466125	0.021847	1.013315	0.0	0	1.880076	0.897406	0.117837	0.853375	0.184494	0.033554	0.001035	0.005482	0.013549	0.029743	0.0	0.119924	0.064570	0.480251	0.063061	0.456688	4.016551	0.456688	0.032066	0.085770	0.272126	0.014872	0.098097	0.883929	0.033554	0.031017	0.044454	0.763034	0.126105	0.763034	0.670848	0.032066	0.085770	0	1203.071834	1145.408596	6.679745	0.449275
3	4.724478	1485.415208	1462.886108	6.668314	1445.388184	1490.610038	1479.008293	3.835582	5.745320	4.368585	0	51.018414	0.477835	4.234044	3.829236	0.133773	16.510645	21.339216	0.371491	0.001249	1.043586	0.0	0	1.882223	0.908064	0.118144	0.843520	0.184101	0.026573	0.000059	0.004180	0.013260	0.030439	0.0	0.117777	0.066324	0.485666	0.063188	0.451146	4.010563	0.451146	0.021068	0.097076	0.178322	0.015219	0.114190	0.884870	0.026573	0.039751	0.039013	0.749537	0.138336	0.749537	0.660555	0.021068	0.097076	0	1226.783508	1175.241288	5.337022	-0.068022
4	3.586955	1464.061123	1450.816528	5.917033	1425.601196	1470.142740	1459.676731	3.619591	4.266036	3.017315	0	49.889533	0.464504	4.194231	4.055550	0.172077	16.485519	21.457441	0.393813	0.000000	0.958231	0.0	0	1.864857	0.918644	0.126777	0.859384	0.184776	0.028541	0.000000	0.005448	0.013060	0.028318	0.0	0.135143	0.049633	0.482277	0.066557	0.451166	4.029806	0.451166	0.059612	0.067165	0.470212	0.014159	0.098534	0.878727	0.028541	0.021092	0.057025	0.767108	0.139157	0.767108	0.670586	0.059612	0.067165	0	1195.862431	1137.912057	5.905188	-0.356520

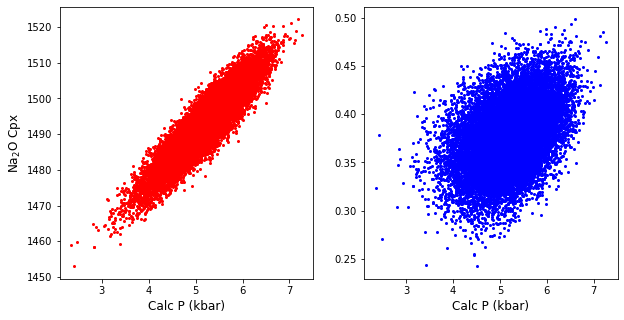
Lets plot these calculations using the Wang et al. (2021) thermometer and barometer

• You can see that despite random input errors, P and T end up correlated in the resulting distribution

• You can also see that pressure is controlled predominantly by the error on the Na2O component, with scatter around this trend

fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,5))
ax1.plot(Calc_PT['P_Wang21_eq1'], Calc_PT['T_Wang21_eq2'], '.r' )
ax2.plot(Calc_PT['P_Wang21_eq1'], Calc_PT['Na2O_Cpx'], '.b' )
ax1.set_xlabel('Calc P (kbar)')
ax2.set_xlabel('Calc P (kbar)')
ax1.set_ylabel('Calc T (K)')
ax1.set_ylabel('Na$_2$O Cpx')

Text(0, 0.5, 'Na$_2$O Cpx')

A more robust way to show this

• If you play around with duplicates = , you’ll see that the more points you ask for, the more spread in pressure space.

• It is more robust to contour results

• First, we show how to do this using hexbin (matplotlib)

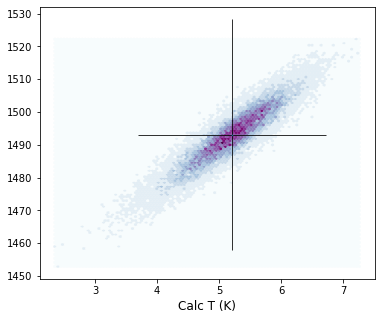
• We underlie the published error on the barometer, at the average calculated composition.

fig, (ax1)  = plt.subplots(1, 1, figsize=(6,5))

ax1.hexbin(Calc_PT['P_Wang21_eq1'],
           Calc_PT['T_Wang21_eq2'],
            cmap=plt.cm.BuPu,
            linewidths=0.2, bins=10)
ax1.set_xlabel('Calc P (kbar)')
ax1.set_xlabel('Calc T (K)')


ax1.errorbar(np.mean(Calc_PT['P_Wang21_eq1']),
             np.mean(Calc_PT['T_Wang21_eq2']),
             xerr=1.52, yerr=35.2,
             fmt='.', ecolor='k', elinewidth=0.8, mfc='k', ms=1)

<ErrorbarContainer object of 3 artists>

But this is still hard to visualize!

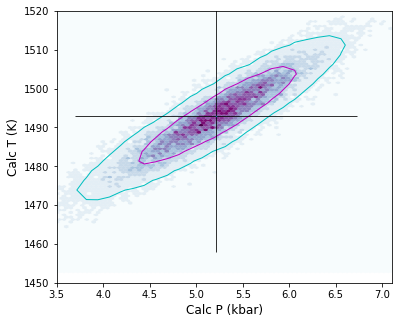
• We can add contours using pyrolite, so we can visualize where 67% of simulations lie, and where 95% of simulations lie

• You will have to play around a bit with the number of bins, and the extent parameter.

• We always plot PT first, then use that to work out the extent, which tells the code where to look for contours in. This only needs to be approximate.

• This step can be slow, if you are using 4-8 Gb of Ram, you might want to reduce the number of duplicates when you make the samples.

• Remember to cite Pyrolite if you use these contours!

from pyrolite.plot import pyroplot

fig, (ax1)  = plt.subplots(1, 1, figsize=(6,5))

# This parameter helps pyrolite converge on the contour positions faster,
# e.g. saying look for contours between 3.5 and 7 kbar
# and between 1470 and 1540 K. You'll need to change this for your particular system
extent1=(3.5, 7, 1470, 1540)
ax1.hexbin(Calc_PT['P_Wang21_eq1'],
           Calc_PT['T_Wang21_eq2'],
            cmap=plt.cm.BuPu,
            linewidths=0.2, bins=10)
ax1.set_xlabel('Calc P (kbar)')
ax1.set_xlabel('Calc T (K)')


Calc_PT.loc[:,
["P_Wang21_eq1", "T_Wang21_eq2"]].pyroplot.density(ax=ax1, contours=[0.67, 0.95], colors=['m', 'c'],
                                                   extent=extent1, cmap="viridis",
                                                   bins=30, label_contours=False)
# Adjust axes limits
ax1.set_xlim([3.5, 7.1])
ax1.set_ylim([1450,  1520])

ax1.errorbar(np.mean(Calc_PT['P_Wang21_eq1']),
             np.mean(Calc_PT['T_Wang21_eq2']),
             xerr=1.52, yerr=35.2,
             fmt='.', ecolor='k', elinewidth=0.8, mfc='k', ms=1)

ax1.set_xlabel('Calc P (kbar)')
ax1.set_ylabel('Calc T (K)')

Text(0, 0.5, 'Calc T (K)')

Lets work out what would happen if we doubled the analytical error on Na2O

• Be patient, this takes a bit of time, its 20,000 calculations!

# First, lets duplicate the error dataframe
df_Cpx_Err_2Na=df_Cpx_Err.copy()
# Lets set Na2O error to 2* what it was
df_Cpx_Err_2Na['Na2O_Cpx_Err']=2*df_Cpx_Err['Na2O_Cpx_Err']
# And lets take sample 0 again
Cpx_1_Err_2Na=df_Cpx_Err_2Na.iloc[[0]].reset_index(drop=True)
# Lets simulate some new Cpxs.
Calc_Cpx_dist_2Na=pt.add_noise_sample_1phase(phase_comp=Cpx_1, phase_err=Cpx_1_Err_2Na,
                                             phase_err_type="Perc", duplicates=20000, err_dist="normal")
# And lets calculate pressures
Calc_PT_2Na=pt.calculate_cpx_only_press_all_eqs(cpx_comps=Calc_Cpx_dist_2Na)

All negative numbers replaced with zeros. If you wish to keep these, set positive=False

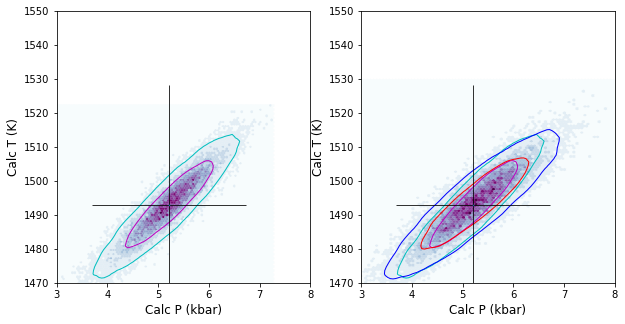
Lets plot these new errors vs. the old errors

• Again, the contours can take ~30s to appear (with 16 Gb of RAM)

fig, (ax1, ax2)  = plt.subplots(1, 2, figsize=(10,5), sharex=True, sharey=True)


extent1=(3.5, 7, 1470, 1540)
ax1.hexbin(Calc_PT['P_Wang21_eq1'],
           Calc_PT['T_Wang21_eq2'],
            cmap=plt.cm.BuPu,
            linewidths=0.2, bins=10)
ax1.set_xlabel('Calc P (kbar)')
ax1.set_xlabel('Calc T (K)')




extent2=(3.5, 7, 1470, 1540)
ax2.hexbin(Calc_PT_2Na['P_Wang21_eq1'],
           Calc_PT_2Na['T_Wang21_eq2'],
            cmap=plt.cm.BuPu,
            linewidths=0.2, bins=10)
ax2.set_xlabel('Calc P (kbar)')
ax2.set_xlabel('Calc T (K)')


Calc_PT.loc[:,
["P_Wang21_eq1", "T_Wang21_eq2"]].pyroplot.density(ax=ax1, contours=[0.67, 0.95], colors=['m', 'c'],
                                                   extent=extent1, cmap="viridis",
                                                   bins=70, label_contours=False)

Calc_PT.loc[:,
["P_Wang21_eq1", "T_Wang21_eq2"]].pyroplot.density(ax=ax2, contours=[0.67, 0.95], colors=['m', 'c'],
                                                   extent=extent1, cmap="viridis",
                                                   bins=70, label_contours=False, width=0.5)

Calc_PT_2Na.loc[:,
["P_Wang21_eq1", "T_Wang21_eq2"]].pyroplot.density(ax=ax2, contours=[0.67, 0.95], colors=['r', 'blue'],
                                                   extent=extent2, cmap="viridis",
                                                   bins=70, label_contours=False)

ax1.errorbar(np.mean(Calc_PT['P_Wang21_eq1']),
             np.mean(Calc_PT['T_Wang21_eq2']),
             xerr=1.52, yerr=35.2,
             fmt='.', ecolor='k', elinewidth=0.8, mfc='k', ms=1)

ax2.errorbar(np.mean(Calc_PT['P_Wang21_eq1']),
             np.mean(Calc_PT['T_Wang21_eq2']),
             xerr=1.52, yerr=35.2,
             fmt='.', ecolor='k', elinewidth=0.8, mfc='k', ms=1)

ax1.set_xlim([3, 8])
ax1.set_ylim([1470,  1550])

ax1.set_xlabel('Calc P (kbar)')
ax1.set_ylabel('Calc T (K)')

ax2.set_xlabel('Calc P (kbar)')
ax2.set_ylabel('Calc T (K)')
ax2.yaxis.set_tick_params(which='both', labelbottom=True)

c:\Users\penny\anaconda3\Lib\site-packages\pyrolite\util\plot\density.py:202: UserWarning: The following kwargs were not used by contour: 'width'
  cs = contour(

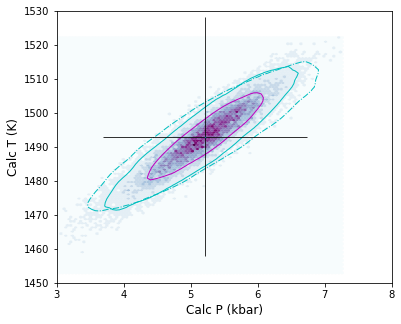
Lets make a pretty figure for publication with just the stated errors for Wang and Putirka thermobarometers, but overlay an additional contour for bigger Na2O errors

# Wang thermobarometers
fig, (ax1)  = plt.subplots(1, figsize=(6,5), sharex=True, sharey=True)

## LHS, Wang et al. 2021
extent1=(3.5, 7, 1470, 1540)
ax1.hexbin(Calc_PT['P_Wang21_eq1'],
           Calc_PT['T_Wang21_eq2'],
            cmap=plt.cm.BuPu,
            linewidths=0.2, bins=10)
ax1.set_xlabel('Calc P (kbar)')
ax1.set_xlabel('Calc T (K)')


Calc_PT.loc[:,
["P_Wang21_eq1", "T_Wang21_eq2"]].pyroplot.density(ax=ax1, contours=[0.67, 0.95], colors=['m', 'c'],
                                                   extent=extent1, cmap="viridis",
                                                   bins=70, label_contours=False)


Calc_PT_2Na.loc[:,
["P_Wang21_eq1", "T_Wang21_eq2"]].pyroplot.density(ax=ax1, contours=[0.95], colors=['c'],
                                                   extent=extent2, cmap="viridis",
                                                   bins=70, label_contours=False,
                                                  linestyles=['-.'])

ax1.errorbar(np.mean(Calc_PT['P_Wang21_eq1']),
             np.mean(Calc_PT['T_Wang21_eq2']),
             xerr=1.52, yerr=35.2,
             fmt='.', ecolor='k', elinewidth=0.8, mfc='k', ms=1)


ax1.set_xlim([3, 8])
ax1.set_ylim([1450,  1530])

ax1.set_xlabel('Calc P (kbar)')
ax1.set_ylabel('Calc T (K)')

ax2.set_xlabel('Calc P (kbar)')
ax2.set_ylabel('Calc T (K)')

ax2.yaxis.set_tick_params(which='both', labelbottom=True)
fig.savefig('Cpx_only_Error.png', dpi=200)

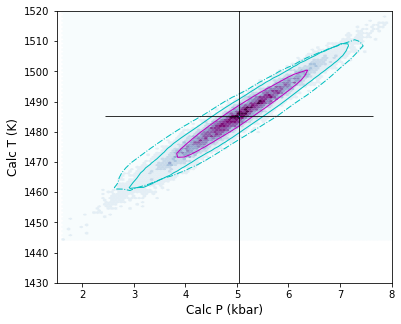
# Putirka Cpx-only barometers
fig, (ax1)  = plt.subplots(1, figsize=(6,5), sharex=True, sharey=True)

## LHS, Wang et al. 2021
extent1=(1, 10, 1430, 1540)
ax1.hexbin(Calc_PT['P_Put_Teq32d_Peq32b'],
           Calc_PT['T_Put_Teq32d_Peq32b'],
            cmap=plt.cm.BuPu,
            linewidths=0.2, bins=10)
ax1.set_xlabel('Calc P (kbar)')
ax1.set_xlabel('Calc T (K)')


Calc_PT.loc[:,
["P_Put_Teq32d_Peq32b", "T_Put_Teq32d_Peq32b"]].pyroplot.density(ax=ax1, contours=[0.67, 0.95], colors=['m', 'c'],
                                                   extent=extent1, cmap="viridis",
                                                   bins=70, label_contours=False)

extent2=(1, 10, 1430, 1540)

Calc_PT_2Na.loc[:,
["P_Put_Teq32d_Peq32b", "T_Put_Teq32d_Peq32b"]].pyroplot.density(ax=ax1, contours=[0.95], colors=['c'],
                                                   extent=extent2, cmap="viridis",
                                                   bins=70, label_contours=False,
                                                  linestyles=['-.'])

ax1.errorbar(np.mean(Calc_PT['P_Put_Teq32d_Peq32b']),
             np.mean(Calc_PT['T_Put_Teq32d_Peq32b']),
             xerr=2.6, yerr=58,
             fmt='.', ecolor='k', elinewidth=0.8, mfc='k', ms=1)


ax1.set_xlim([1.5, 8])
ax1.set_ylim([1430,  1520])

ax1.set_xlabel('Calc P (kbar)')
ax1.set_ylabel('Calc T (K)')

ax2.set_xlabel('Calc P (kbar)')
ax2.set_ylabel('Calc T (K)')

ax2.yaxis.set_tick_params(which='both', labelbottom=True)
fig.savefig('Cpx_only_Error_Put.png', dpi=200)

Lets calculate the statistics for various noise simulations

Stats_P=pt.av_noise_samples_series(Calc_PT['P_Wang21_eq1'], Calc_PT['Sample_ID_Cpx_Num'])
Stats_P

	Sample	# averaged	Mean_calc	Median_calc	St_dev_calc	St_dev_calc_from_percentiles	Max_calc	Min_calc
0	0.0	20000	5.224174	5.243925	0.581436	0.574622	7.112735	2.418245

Stats_T=pt.av_noise_samples_series(Calc_PT['T_Wang21_eq2'], Calc_PT['Sample_ID_Cpx_Num'])
Stats_T

	Sample	# averaged	Mean_calc	Median_calc	St_dev_calc	St_dev_calc_from_percentiles	Max_calc	Min_calc
0	0.0	20000	1493.217726	1493.365316	8.596538	8.501955	1525.253951	1453.330584

Stats_T=pt.av_noise_samples_series(Calc_PT_2Na['T_Wang21_eq2'], Calc_PT_2Na['Sample_ID_Cpx_Num'])
Stats_T

	Sample	# averaged	Mean_calc	Median_calc	St_dev_calc	St_dev_calc_from_percentiles	Max_calc	Min_calc
0	0.0	20000	1493.243792	1493.461736	9.229113	9.180253	1530.644994	1453.990044

Stats_P=pt.av_noise_samples_series(Calc_PT_2Na['P_Wang21_eq1'], Calc_PT_2Na['Sample_ID_Cpx_Num'])
Stats_P

	Sample	# averaged	Mean_calc	Median_calc	St_dev_calc	St_dev_calc_from_percentiles	Max_calc	Min_calc
0	0.0	20000	5.22653	5.244425	0.721283	0.713538	8.01063	2.172848

Stats_P_Put=pt.av_noise_samples_series(Calc_PT_2Na['P_Put_Teq32d_Peq32b'], Calc_PT_2Na['Sample_ID_Cpx_Num'])
Stats_P_Put

	Sample	# averaged	Mean_calc	Median_calc	St_dev_calc	St_dev_calc_from_percentiles	Max_calc	Min_calc
0	0.0	20000	5.00325	5.019843	0.952609	0.947076	8.946914	0.761413

Stats_P_Put=pt.av_noise_samples_series(Calc_PT['P_Put_Teq32d_Peq32b'], Calc_PT['Sample_ID_Cpx_Num'])
Stats_P_Put

	Sample	# averaged	Mean_calc	Median_calc	St_dev_calc	St_dev_calc_from_percentiles	Max_calc	Min_calc
0	0.0	20000	5.035922	5.036038	0.844282	0.83978	8.088378	1.862193

Stats_P_Put=pt.av_noise_samples_series(Calc_PT['T_Put_Teq32d_Peq32b'], Calc_PT['Sample_ID_Cpx_Num'])
Stats_P_Put

	Sample	# averaged	Mean_calc	Median_calc	St_dev_calc	St_dev_calc_from_percentiles	Max_calc	Min_calc
0	0.0	20000	1485.247841	1485.337527	9.574996	9.55245	1520.120853	1443.237187