This page was generated from
docs/Examples/Other_features/Calibration_Plot_Examples.ipynb.
Interactive online version:
.
Assessing Calibration Ranges of models
This notebook shows how users can plot their data amonst the calibration range of different models to assess whether they are within the calibration range
You can download the excel spreadsheet here: https://github.com/PennyWieser/Thermobar/blob/main/docs/Examples/Other_features/Example_Liq_Px_Amp.xlsx
[1]:
#!pip install Thermobar --upgrade
[2]:
# First, load various python things. If you haven't installed Thermobar do so now
# by removing the # next to !pip install
#!pip install Thermobar
import Thermobar as pt
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
pt.__version__
[2]:
'1.0.34dev'
Step 1: Load in data from your system
in this case some pyroxene, amphibole and liquid data.
[3]:
out=pt.import_excel('Example_Liq_Px_Amp.xlsx', sheet_name="Liquid")
Liquids1=out['Liqs']
out2=pt.import_excel('Example_Liq_Px_Amp.xlsx', sheet_name="Pyroxene")
Cpxs1=out2['Cpxs']
out3=pt.import_excel('Example_Liq_Px_Amp.xlsx', sheet_name="Amphibole")
Amps1=out3['Amps']
c:\Users\penny\anaconda3\Lib\site-packages\openpyxl\worksheet\_read_only.py:79: UserWarning: Unknown extension is not supported and will be removed
for idx, row in parser.parse():
Step 2: The two ways to use these functions
You have two options, you can either use the function “return_cali_dataset” which will return the calibration dataset of each model so you can make whatever plots you want.
Or, you can use the prebuilt plotting function “generic_cali_plot” which allows you to specify a model, and an x and y paramter, and will make the plot for you.
You can see the different options using the help function
We will add as many calibratoin datasets as we can find - if you have one, please reach out! So far, the supported ones are listed here under “model” for each phase
[4]:
help(pt.generic_cali_plot)
Help on function generic_cali_plot in module Thermobar.calibration_plots:
generic_cali_plot(df, model=None, x=None, y=None, P_kbar=None, T_K=None, figsize=(7, 5), shape_cali='o', mfc_cali='white', mec_cali='k', ms_cali=5, shape_data='^', mfc_data='red', alpha_cali=1, alpha_data=1, mec_data='k', ms_data=10, order='cali bottom', save_fig=False, fig_name=None, dpi=200)
This function plots your compositions amongst the calibration dataset for a variety of models where we could
obtain the exact calibration dataset. see model for option.
Parameters
-------
df: pandas DataFrame
dataframe of your compositions, e.g. a dataframe of Cpx composition
x and y: str
What you want to plotted against each other. E.g. x="SiO2_Cpx", y="Al2O3_Cpx"
model: str
AMPHIBOLE:
Ridolfi2021: Ridolfi et al. (2012)
Putirka2016: Putirka (2016)
Mutch2016: Mutch et al. (2016)
Zhang2017: Zhang et al. (2017)
CPX:
Putirka2008: Putirka (2008) - entire database for Cpx-Liq,
(not used for all equations).
Masotta2013: Masotta et al. (2013)
Neave2017: Neave and Putirka (2017) for Cpx-Liq
Brugman2019: Brugman and Till 2019
Petrelli2020: Petrelli et al. (2020) for Cpx and Cpx-Liq
Wang2021: Wang et al. (2021) Cpx-only,but contains Liq compositions too.
Jorgenson2022: Jorgenson et al. (2022) Cpx-Liq and Cpx-only,
PLAGIOCLASE
Waters2015: Waters and Lange (2015) for plag-liq hygrometry
Masotta2019: Masotta et al. (2019) plag-liq hygrometry
P_kbar and T_K: pd.Series
if you want to plot calculated pressure and temperature against the calibration range,
specify those panda series here, and it will append them onto your dataframe
Plot customization options.
-------
figsize: (x, y)
figure size
order: 'cali top' or 'cali bottom':
whether cali or user data is plotted ontop. default, cali data bottom
shape_cali, shape_data:
matplotlib symbol, e.g. shape_cali='o' and shape_data='^' are the defaults
ms_cali, ms_data:
marker size for cali and user data
mfc_cali, mfc_data:
marker face color for cali and data (can be different)
mec_cali, mfc_data:
marker edge color for cali and data.
alpha_cali, alpha_data:
transparency of symbols
save_fig: bool
if True, saves figure
Uses fig_name to give filename, dpi to give dpi
[5]:
sup_models=['Ridolfi2021', 'Zhang2017', 'Putirka2016', 'Mutch2016', 'Shea2022', 'Wang2021', 'Petrelli2020', 'Putirka2008', 'Neave2017',
'Brugman2019', 'Masotta2013', 'Jorgenson2022' , 'Waters2015', 'Masotta2019']
for model in sup_models:
pt.return_cali_dataset(model=model)
Example 1 - Amphibole
Example 1a- First, lets use the prebuilt plot functions
[26]:
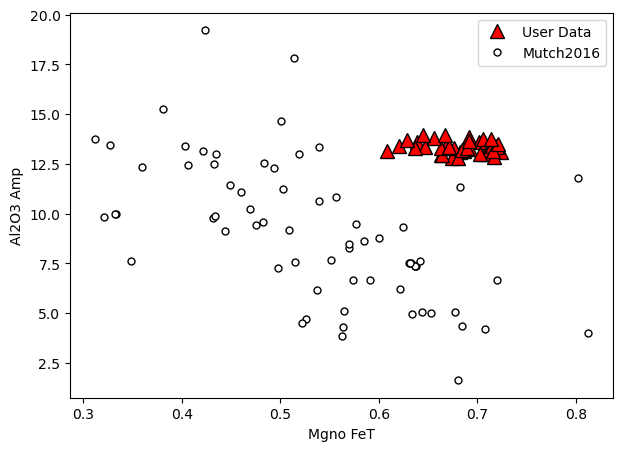
## Example in manuscript - v simple
a=pt.generic_cali_plot(df=Amps1, model="Mutch2016",
x='Mgno_FeT', y='Al2O3_Amp')
a.savefig('Cali_plot_amphibole.png', dpi=200)
[7]:
# Here we specify we want mutch, that we want calibration data
# on the bottom, and alpha (Transparency) at 80% for our data
a=pt.generic_cali_plot(df=Amps1, model="Mutch2016",
x='Mgno_FeT', y='Al2O3_Amp', order="cali bottom",
alpha_cali=1, alpha_data=0.8)
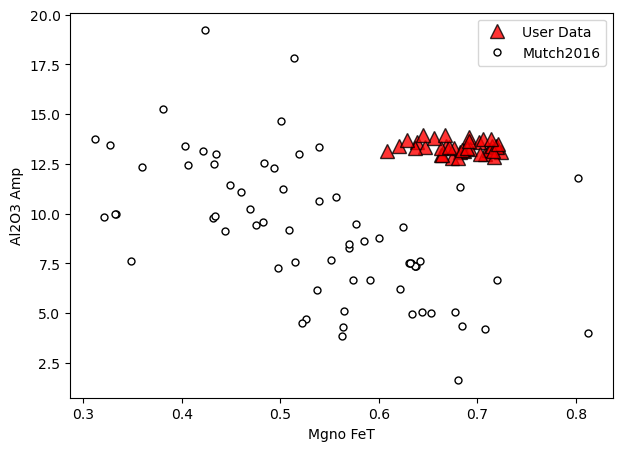
Here we specify we want mutch, that we want calibration data on the bottom, and alpha (Transparency) at 80% for our data
[8]:
a=pt.generic_cali_plot(df=Amps1, model="Ridolfi2021",
x='Mgno_FeT', y='Al2O3_Amp', order="cali bottom",
alpha_cali=1, alpha_data=0.8)
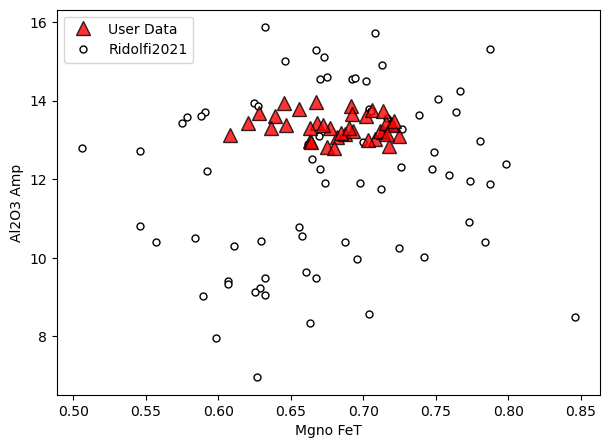
Example 1b: lets load the calibration datasets for Mutch and Ridolfi
[9]:
Cali_Dataset_Mutch=pt.return_cali_dataset(model="Mutch2016")
Cali_Dataset_Ridolfi=pt.return_cali_dataset(model="Ridolfi2021")
Now we can use matplotlib to make whatever plot we want
[10]:
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,5))
ax1.plot(Cali_Dataset_Mutch['Na2O_Amp'], Cali_Dataset_Mutch['MgO_Amp'],
'ok', mfc='white')
ax1.plot(Amps1['Na2O_Amp'], Amps1['MgO_Amp'], '^k', mfc='red')
ax1.set_xlabel('Na$_2$O Amp')
ax1.set_ylabel('MgO Amp')
ax2.plot(Cali_Dataset_Ridolfi['Na2O_Amp'], Cali_Dataset_Ridolfi['MgO_Amp'],
'ok', mfc='white')
ax2.plot(Amps1['Na2O_Amp'], Amps1['MgO_Amp'], '^k', mfc='red')
ax2.set_xlabel('Na$_2$O Amp')
ax2.set_ylabel('MgO Amp')
[10]:
Text(0, 0.5, 'MgO Amp')
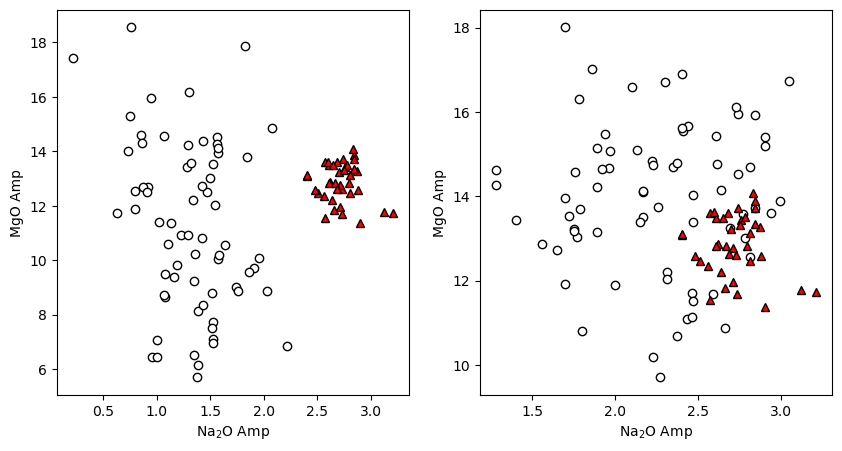
Example 1c - What if we want to compare pressures and temperatures to the cali dataset?
First, we need to calculate the P and Ts using the equations.
[11]:
P_Mutch=pt.calculate_amp_only_press(amp_comps=Amps1, equationP="P_Mutch2016")
P_Ridolfi=pt.calculate_amp_only_press_temp(amp_comps=Amps1,
equationP="P_Ridolfi2021",
equationT="T_Ridolfi2012")
[12]:
P_Ridolfi.head()
[12]:
| P_kbar_calc | T_K_calc | Input_Check | Fail Msg | classification | equation | SiO2_Amp | TiO2_Amp | Al2O3_Amp | FeOt_Amp | MnO_Amp | MgO_Amp | CaO_Amp | Na2O_Amp | K2O_Amp | Cr2O3_Amp | F_Amp | Cl_Amp | Sample_ID_Amp | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 4.922720 | 1301.307668 | True | kaersutite | (1b+1c)/2 | 40.46 | 5.96 | 12.97 | 11.18 | 0.1201 | 12.35 | 11.54 | 2.56 | 1.1721 | 0.0093 | 0.0 | 0.0 | Lava_1_amph-2_ | |
| 1 | 5.751972 | 1337.114450 | True | kaersutite | 1a | 40.85 | 6.14 | 13.08 | 10.70 | 0.2122 | 12.88 | 11.35 | 2.62 | 0.8556 | 0.0069 | 0.0 | 0.0 | Lava_1-8_ | |
| 2 | 9.288183 | 1344.043447 | True | kaersutite | 1e | 40.76 | 5.54 | 13.13 | 13.08 | 0.1802 | 11.38 | 11.38 | 2.90 | 0.8943 | 0.0022 | 0.0 | 0.0 | Lava_1-16_ | |
| 3 | 7.976460 | 1335.292103 | True | kaersutite | 1d | 40.62 | 5.60 | 13.42 | 11.16 | 0.1066 | 12.61 | 11.57 | 2.73 | 0.9961 | 0.0000 | 0.0 | 0.0 | Lava_1-20_ | |
| 4 | 8.048350 | 1333.351123 | True | kaersutite | 1d | 39.99 | 5.49 | 13.60 | 12.03 | 0.1600 | 11.96 | 11.56 | 2.71 | 1.0031 | 0.0092 | 0.0 | 0.0 | Lava_1-24_ |
Now we can use the generic plot function to add the P_kbar onto the dataframe
[13]:
a=pt.generic_cali_plot(df=Amps1, model="Ridolfi2021",
x='P_kbar', y='Mgno_FeT', P_kbar=P_Ridolfi['P_kbar_calc'],
order="cali bottom",
alpha_cali=1, alpha_data=0.8)
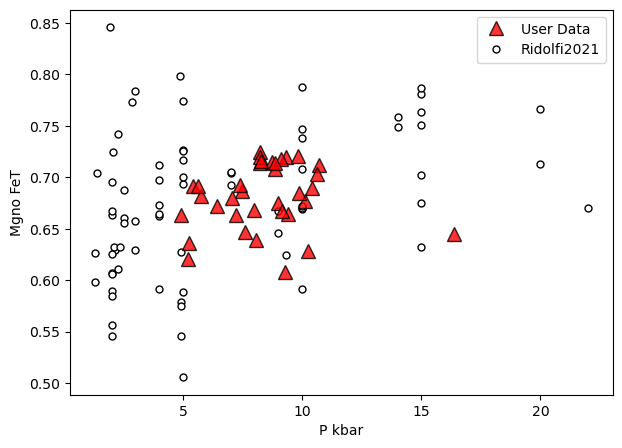
Or, for Ridolfi, plot pressure and temperature
[14]:
a=pt.generic_cali_plot(df=Amps1, model="Ridolfi2021",
x='P_kbar', y='T_K', P_kbar=P_Ridolfi['P_kbar_calc'],
T_K=P_Ridolfi['T_K_calc'],
order="cali bottom",
alpha_cali=1, alpha_data=0.4)
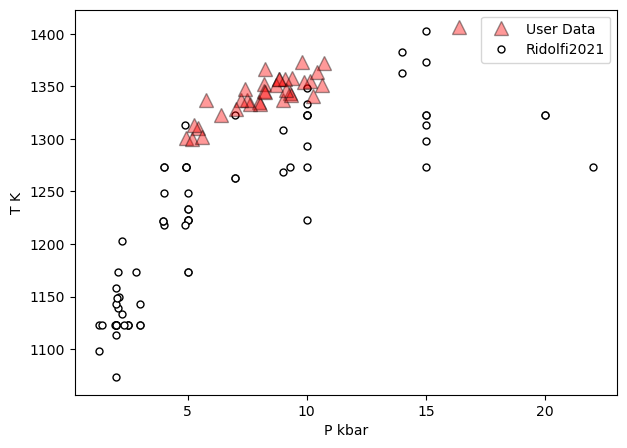
[15]:
a=pt.generic_cali_plot(df=Amps1, model="Mutch2016",
x='P_kbar', y='Mgno_FeT', P_kbar=P_Mutch['P_kbar_calc'],
order="cali bottom",
alpha_cali=1, alpha_data=0.8)
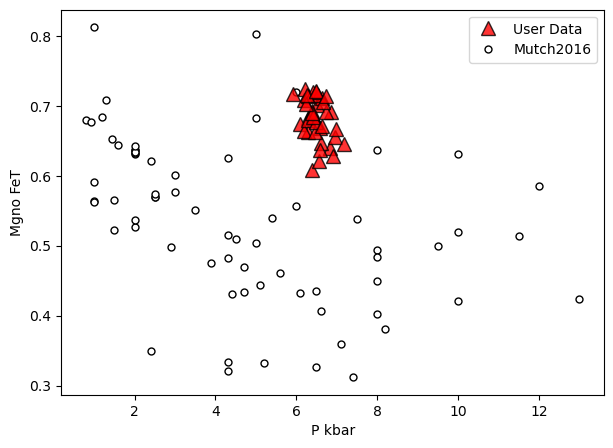
Example 2 - Cpx
Example 2a: Loading the various calibration datasets, making plots using mpl
[16]:
Rid_Cali=pt.return_cali_dataset(model='Ridolfi2021')
Rid_Cali.head()
[16]:
| Unnamed: 0 | Reference | spot/exp. | T | P | H2O_Liq | ∆NNO | logfO2 | Unnamed: 7 | SiO2_Amp | ... | Total | Fail Msg | Input_Check | Mgno_Fe2 | Mgno_FeT | Na_calc | B_Sum | A_Sum | class | classification | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | Adam & Green (1994) | 1446 | 1050 | 1500.0 | NaN | NaN | NaN | NaN | 42.43 | ... | NaN | NaN | True | 0.868273 | 0.780512 | 0.258108 | 2.0 | 0.717443 | NaN | Mg-hastingsite |
| 1 | 1 | Adam & Green (1994) | 1447 | 1050 | 1000.0 | NaN | NaN | NaN | NaN | 41.19 | ... | NaN | NaN | True | 0.885676 | 0.747414 | 0.194505 | 2.0 | 0.757125 | NaN | Mg-hastingsite |
| 2 | 2 | Gardner et al. (1995) | G-14b | 850 | 250.0 | 6.3 | 1.191313 | -11.594939 | NaN | 45.69 | ... | NaN | NaN | True | 0.899146 | 0.660164 | 0.363048 | 2.0 | 0.165110 | NaN | Mg-Hornblende |
| 3 | 3 | Gardner et al. (1995) | G-15a | 850 | 250.0 | 5.7 | 1.190000 | -11.596251 | NaN | 45.56 | ... | NaN | NaN | True | 0.918743 | 0.687599 | 0.328591 | 2.0 | 0.234784 | NaN | Tschermakitic pargasite |
| 4 | 4 | Gardner et al. (1995) | G-14a | 850 | 250.0 | 7.0 | 0.986417 | -11.799834 | NaN | 45.65 | ... | NaN | NaN | True | 0.872857 | 0.655715 | 0.363498 | 2.0 | 0.202943 | NaN | Tschermakitic pargasite |
5 rows × 82 columns
[17]:
Brugman_Cali=pt.return_cali_dataset(model='Brugman2019')
Petrelli_Cali=pt.return_cali_dataset(model='Petrelli2020')
Neave_Cali=pt.return_cali_dataset(model='Neave2017')
Masotta_Cali=pt.return_cali_dataset(model='Masotta2013')
# And calculate Cpx components for loaded cpx
input_cpx_comps=pt.calculate_clinopyroxene_components(cpx_comps=Cpxs1)
[18]:
## Lets have a look at these
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,4))
ax1.plot(Masotta_Cali['Mgno_Cpx'],
Masotta_Cali['Na2O_Liq']+Masotta_Cali['K2O_Liq'],
'pk', mfc='yellow', ms=5, alpha=0.6, label='Masotta2013')
ax1.plot(Petrelli_Cali['Mgno_Cpx'],
Petrelli_Cali['Na2O_Liq']+Petrelli_Cali['K2O_Liq'],
'sk', mfc='blue', ms=3, alpha=0.6, label='Petrelli2020')
ax1.plot(Neave_Cali['Mgno_Cpx'],
Neave_Cali['Na2O_Liq']+Neave_Cali['K2O_Liq'],
'sk', mfc='red', label='Neave2017')
ax1.plot(Brugman_Cali['Mgno_Cpx'],
Brugman_Cali['Na2O_Liq']+Brugman_Cali['K2O_Liq'],
'ok', mfc='white', label='Brugman2019')
# Then calc
ax1.legend()
ax1.set_xlabel('Mg# (Cpx)')
ax1.set_ylabel('Na$_2$O + K$_2$O (Liq)')
y2='T_K'
x2='P_kbar'
ax2.plot(Masotta_Cali[x2],
Masotta_Cali[y2],
'pk', mfc='yellow', ms=5, alpha=0.6, label='Masotta2013')
ax2.plot(Petrelli_Cali[x2],
Petrelli_Cali[y2],
'sk', mfc='blue', ms=3, alpha=0.6, label='Petrelli2020')
ax2.plot(Neave_Cali[x2],
Neave_Cali[y2],
'sk', mfc='red', label='Neave2017')
ax2.plot(Brugman_Cali[x2],
Brugman_Cali[y2],
'ok', mfc='white', label='Brugman2019')
ax2.set_xlabel(x2)
ax2.set_ylabel(y2)
[18]:
Text(0, 0.5, 'T_K')
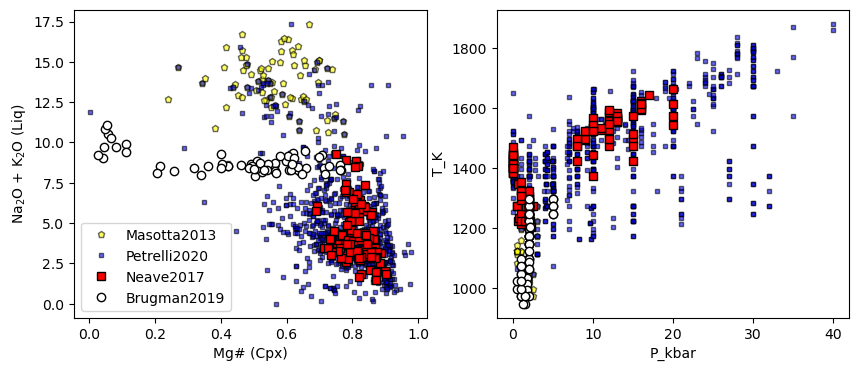
Example 2b: Using built in functions for plotting
[19]:
a=pt.generic_cali_plot(df=Cpxs1, model="Neave2017",
x='Mgno_Cpx', y='Na2O_Cpx',
order="cali bottom",
alpha_cali=1, alpha_data=0.2)
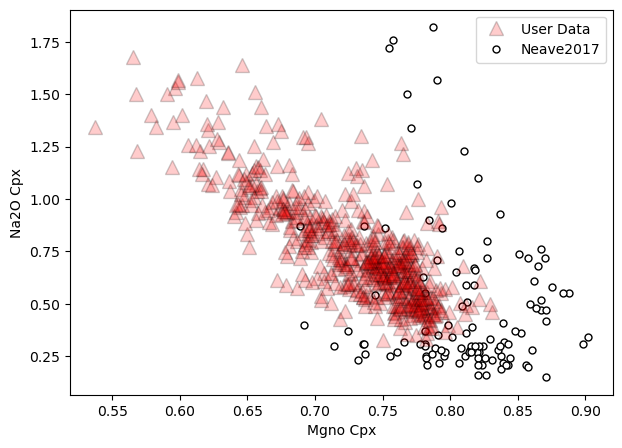
Lets say calculate P and T, then make plots with that
[20]:
PT_Pet20=pt.calculate_cpx_only_press_temp(cpx_comps=Cpxs1, equationP="P_Petrelli2020_Cpx_only",
equationT="T_Petrelli2020_Cpx_only")
Youve selected a P-independent function
Youve selected a T-independent function
[21]:
a=pt.generic_cali_plot(df=Cpxs1, model="Petrelli2020",
x='P_kbar', y='T_K', P_kbar=PT_Pet20['P_kbar_calc'],
T_K=PT_Pet20['T_K_calc'],
order="cali bottom",
alpha_cali=1, alpha_data=0.2)
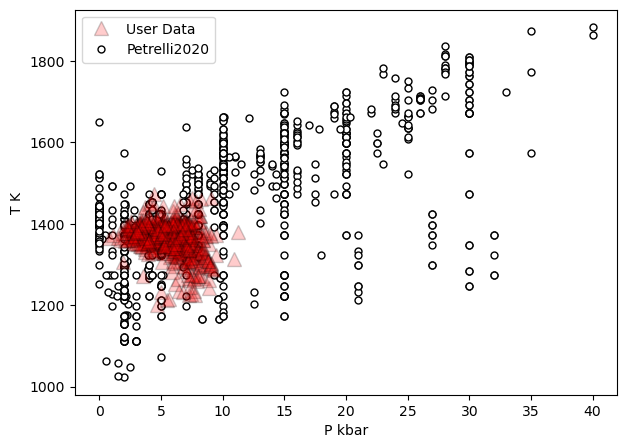
Example 3 - Assessing matched liquid - Cpx pairs
[22]:
# First, lets calculate matched Cpx-Liq pairs.
cpx_liq_out=pt.calculate_cpx_liq_press_temp_matching(cpx_comps=Cpxs1, liq_comps=Liquids1,
equationT="T_Mas2013_Talk2012",
equationP="P_Mas2013_Palk2012")
all_matches=cpx_liq_out['All_PTs']
av_matches=cpx_liq_out['Av_PTs']
Considering N=574 Cpx & N=51 Liqs, which is a total of N=29274 Liq-Cpx pairs, be patient if this is >>1 million!
Youve selected a P-independent function
Youve selected a P-independent function
2207 Matches remaining after initial Kd filter. Now moving onto iterative calculations
Youve selected a P-independent function
Youve selected a T-independent function
Youve selected a T-independent function
Finished calculating Ps and Ts, now just averaging the results. Almost there!
Done!!! I found a total of N=1244 Cpx-Liq matches using the specified filter. N=358 Cpx out of the N=574 Cpx that you input matched to 1 or more liquids
[23]:
## Lets have a look at these
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,4))
ax1.plot(Masotta_Cali['Mgno_Cpx'],
Masotta_Cali['Na2O_Liq']+Masotta_Cali['K2O_Liq'],
'pk', mfc='yellow', ms=5, alpha=0.6, label='Masotta2013')
ax1.plot(Petrelli_Cali['Mgno_Cpx'],
Petrelli_Cali['Na2O_Liq']+Petrelli_Cali['K2O_Liq'],
'sk', mfc='blue', ms=3, alpha=0.6, label='Petrelli2020')
ax1.plot(Neave_Cali['Mgno_Cpx'],
Neave_Cali['Na2O_Liq']+Neave_Cali['K2O_Liq'],
'sk', mfc='red', label='Neave2017', alpha=0.6)
ax1.plot(Brugman_Cali['Mgno_Cpx'],
Brugman_Cali['Na2O_Liq']+Brugman_Cali['K2O_Liq'],
'ok', mfc='white', label='Brugman2019', alpha=0.6)
ax1.plot(all_matches['Mgno_Cpx'], all_matches['Na2O_Liq']+all_matches['K2O_Liq'],
'*c', ms=10, mfc='None', label='Data', alpha=1)
# Then calc
ax1.legend()
ax1.set_xlabel('Mg# (Cpx)')
ax1.set_ylabel('Na$_2$O + K$_2$O (Liq)')
y2='T_K'
x2='P_kbar'
ax2.plot(Masotta_Cali[x2],
Masotta_Cali[y2],
'pk', mfc='yellow', ms=5, label='Masotta2013', alpha=0.6)
ax2.plot(Petrelli_Cali[x2],
Petrelli_Cali[y2],
'sk', mfc='blue', ms=3, label='Petrelli2020', alpha=0.6)
ax2.plot(Neave_Cali[x2],
Neave_Cali[y2],
'sk', mfc='red', label='Neave2017', alpha=0.6)
ax2.plot(Brugman_Cali[x2],
Brugman_Cali[y2],
'ok', mfc='white', label='Brugman2019', alpha=0.6)
ax2.plot( all_matches['P_kbar_calc'],all_matches['T_K_calc'],
'*c', ms=10, mfc='None', label='Data', alpha=1)
ax2.set_xlabel(x2)
ax2.set_ylabel(y2)
[23]:
Text(0, 0.5, 'T_K')
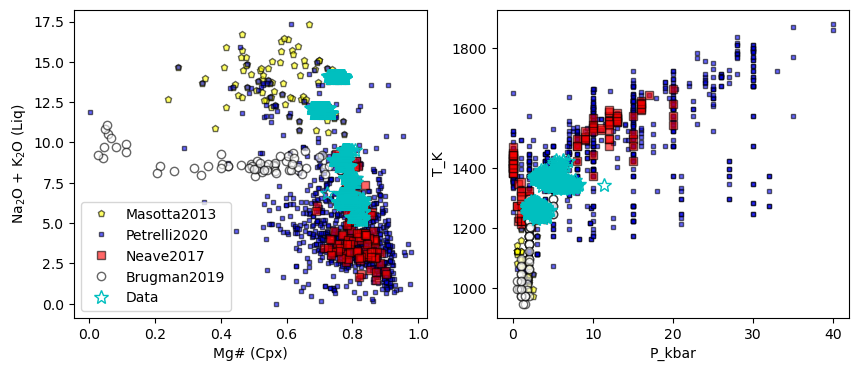
[24]:
a=pt.generic_cali_plot(df=all_matches, model="Petrelli2020",
x='Mgno_Cpx', y='T_K', P_kbar=all_matches['P_kbar_calc'],
T_K=all_matches['T_K_calc'],
order="cali bottom",
alpha_cali=1, alpha_data=0.2)
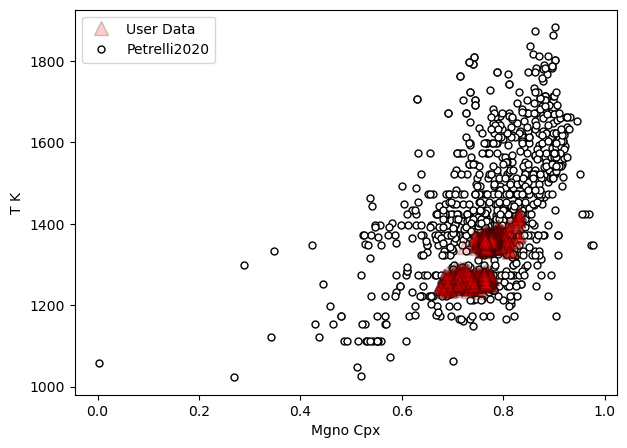
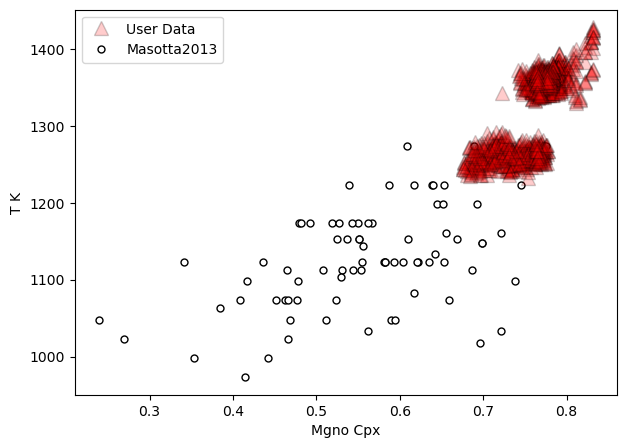
[25]:
a=pt.generic_cali_plot(df=all_matches, model="Masotta2013",
x='Mgno_Cpx', y='T_K',
T_K=all_matches['T_K_calc'],
order="cali bottom",
alpha_cali=1, alpha_data=0.2)
[ ]:
[ ]:
[ ]: