This page was generated from docs/Examples/Opx_and_Opx_Liq_Thermobarometry/Opx_Liq_Thermobarometry.ipynb. Interactive online version: .

Orthopyroxene-only and Liquid thermobarometry.

This notebook shows how to perform opx-only and opx-liq thermobarometry
You can download the spreadsheet with data here: https://github.com/PennyWieser/Thermobar/blob/main/docs/Examples/Opx_and_Opx_Liq_Thermobarometry/Opx_Liq_Example.xlsx

You need to install Thermobar once on your machine, if you haven’t done this yet, uncomment the line below (remove the #)

[1]:

#!pip install Thermobar

First, load the necessary python things

[2]:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import Thermobar as pt

Now, load the data

[3]:

out=pt.import_excel('Opx_Liq_Example.xlsx', sheet_name="Paired_Opx_Liq")
my_input=out['my_input']
Liqs=out['Liqs']
Opxs=out['Opxs']

At any point, you can do help(pt.function) to get some more information

[4]:

help(pt.calculate_opx_liq_temp)

Help on function calculate_opx_liq_temp in module Thermobar.orthopyroxene_thermobarometry:

calculate_opx_liq_temp(*, equationT, opx_comps=None, liq_comps=None, meltmatch=None, P=None, eq_tests=False, Fe3Fet_Liq=None, H2O_Liq=None)
    Orthopyroxene-Liquid thermometer, user specifies equation,
    and calculates temperature in Kelvin.  Also has option to calculate equilibrium tests.

    Parameters
    -------

    opx_comps: pandas.DataFrame
        Orthopyroxene compositions with column headings SiO2_Opx, MgO_Opx etc.

    liq_comps: pandas.DataFrame
        Liquid compositions with column headings SiO2_Liq, MgO_Liq etc.

    meltmatch: pandas.DataFrame
        Combined Opx-Liquid compositions. Used for "melt match" functionality.

    EquationT: str
        Choice of equation:
        |  T_Opx_Beatt1993
        |  T_Put2008_eq28a
        |  T_Put2008_eq28b_opx_sat


    P: float, int, pandas.Series, str  ("Solve")
        Pressure in kbar
        Only needed for P-sensitive thermometers.
        If enter P="Solve", returns a partial function
        Else, enter an integer, float, or panda series

    eq_tests: bool
        If False (default), returns temperature as a panda series
        If True, returns prsesure, Kd Fe-Mg for liq-opx,
        as well as user-entered opx and liq comps as a panda dataframe.

    Returns
    -------
    If eq_tests=False
        pandas.Series: Pressure in kbar (if eq_tests=False)
    If eq_tests=True
        pandas.DataFrame: Pressure in kbar + Kd-Fe-Mg + opx+liq comps

Alternatively, you can access the function names as well as the inputs like this:

[5]:

pt.Opx_Liq_T_funcs

[5]:

{<function Thermobar.orthopyroxene_thermobarometry.T_Beatt1993_opx(P, *, Ca_Liq_cat_frac, Fet_Liq_cat_frac, Mg_Liq_cat_frac, Mn_Liq_cat_frac, Al_Liq_cat_frac, Ti_Liq_cat_frac)>,
 <function Thermobar.orthopyroxene_thermobarometry.T_Put2008_eq28a(P, *, H2O_Liq, ln_Fm2Si2O6_liq, Mg_Liq_cat_frac, K_Liq_cat_frac, Fet_Liq_cat_frac, Fet_Opx_cat_6ox)>,
 <function Thermobar.orthopyroxene_thermobarometry.T_Put2008_eq28b_opx_sat(P, *, H2O_Liq, Mg_Liq_cat_frac, Ca_Liq_cat_frac, K_Liq_cat_frac, Mn_Liq_cat_frac, Fet_Liq_cat_frac, Fet_Opx_cat_6ox, Al_Liq_cat_frac, Ti_Liq_cat_frac, Mg_Number_Liq_NoFe3)>}

[6]:

pt.Opx_Liq_P_funcs

[6]:

{<function Thermobar.orthopyroxene_thermobarometry.P_Put2008_eq29a(T, *, Si_Liq_cat_frac, Mg_Liq_cat_frac, Fet_Opx_cat_6ox, FmAl2SiO6, Na_Liq_cat_frac, Al_Liq_cat_frac, K_Liq_cat_frac, H2O_Liq, NaAlSi2O6)>,
 <function Thermobar.orthopyroxene_thermobarometry.P_Put2008_eq29b(T, *, ln_FmAl2SiO6_liq, Al_Liq_cat_frac, Mg_Liq_cat_frac, Fet_Liq_cat_frac, Si_Opx_cat_6ox, Fet_Opx_cat_6ox, Na_Liq_cat_frac, K_Liq_cat_frac, H2O_Liq)>,
 <function Thermobar.orthopyroxene_thermobarometry.P_Put_Felsic_Opx(T=None, *, Al2O3_Opx, Al2O3_Liq)>,
 <function Thermobar.orthopyroxene_thermobarometry.P_Put_Global_Opx(T=None, *, MgO_Liq, Al2O3_Opx, Al2O3_Liq, Na2O_Liq, K2O_Liq)>}

Example 1 - temperature for a known pressure and water content

1a - Equation 28a, fixed pressure

Here, we calculate temperature using the H2O content given in the H2O_Liq column (the default), and P=5 kbar
We choose T_Put2008_eq28a for temperature

[8]:

Temp_T28a=pt.calculate_opx_liq_temp(opx_comps=Opxs, liq_comps=Liqs,
                                    equationT="T_Put2008_eq28a", P=5)-273.15
Temp_T28a

[8]:

0    1117.972951
1    1117.985930
2    1062.099511
3    1077.766688
4    1037.866109
dtype: float64

1b - As above, but overwriting the input spreadsheet water content with an integer.

[9]:

Temp_T28a_0H2O=pt.calculate_opx_liq_temp(opx_comps=Opxs, liq_comps=Liqs,
                        equationT="T_Put2008_eq28a", P=5, H2O_Liq=0)-273.15 # convert to C
Temp_T28a_0H2O

[9]:

0    1178.028325
1    1219.414583
2    1153.227807
3    1171.722220
4    1124.713370
dtype: float64

1c - we can also specify eq_tests=True to get a full dataframe back with all the components, as well as a number of equilibrium test values

[10]:

Temp_T28a_0H2O_EqTests=pt.calculate_opx_liq_temp(opx_comps=Opxs, liq_comps=Liqs,
                        equationT="T_Put2008_eq28a", P=5, H2O_Liq=0, eq_tests=True)
Temp_T28a_0H2O_EqTests

[10]:

	T_K_calc	eq_tests_Kd_Fe_Mg_Fet	eq_tests_Kd_Fe_Mg_Fe2	SiO2_Liq	Kd Eq (Put2008+-0.06)	TiO2_Liq	Al2O3_Liq	FeOt_Liq	MnO_Liq	MgO_Liq	...	Di_Opx	Mgno_OPX	ln_Fm2Si2O6_liq	ln_FmAl2SiO6_liq	Kd_Fe_Mg_Fet	Kd_Fe_Mg_Fe2	Ideal_Kd	Delta_Kd_Fe_Mg_Fe2	Mgno_Liq_noFe3	Mgno_Liq_Fe2
0	1451.178325	0.251582	0.251582	51.1	Y	0.93	17.5	8.91	0.18	6.09	...	0.028142	0.828850	5.211708	-2.879647	0.251582	0.251582	0.304877	0.053295	0.549218	0.549218
1	1492.564583	0.165104	0.165104	51.5	N	1.19	19.2	8.70	0.19	4.98	...	0.068126	0.860725	5.202722	3.931199	0.165104	0.165104	0.303256	0.138151	0.505036	0.505036
2	1426.377807	0.187634	0.187634	59.1	N	0.54	19.1	5.22	0.19	3.25	...	0.074962	0.855382	5.851735	4.175071	0.187634	0.187634	0.277184	0.089550	0.526025	0.526025
3	1444.872220	0.211297	0.211297	52.5	N	0.98	19.2	8.04	0.20	4.99	...	0.053125	0.839637	5.426741	1.519044	0.211297	0.211297	0.300632	0.089335	0.525239	0.525239
4	1397.863370	0.144506	0.144506	56.2	N	0.34	20.4	5.88	0.20	2.58	...	0.033103	0.844054	6.297377	2.489832	0.144506	0.144506	0.290284	0.145777	0.438875	0.438875

5 rows × 92 columns

Example 2 - Calculating pressure for a known temperature

2a - Pressure using equation 29a at 1300 K

[11]:

Temp_P29a=pt.calculate_opx_liq_press(opx_comps=Opxs, liq_comps=Liqs,
                                    equationP="P_Put2008_eq29a", T=1300)
Temp_P29a

[11]:

0     2.401637
1    12.237354
2     9.658047
3     5.585392
4     5.739632
dtype: float64

2b - Overwrite input water content with zero. Return equilibrium tests.

[12]:

Temp_P29a_0H2O=pt.calculate_opx_liq_press(opx_comps=Opxs, liq_comps=Liqs,
    equationP="P_Put2008_eq29a", T=1300, H2O_Liq=0, eq_tests=True)
Temp_P29a_0H2O

[12]:

	SiO2_Liq	P_kbar_calc	eq_tests_Kd_Fe_Mg_Fet	eq_tests_Kd_Fe_Mg_Fe2	Kd Eq (Put2008+-0.06)	TiO2_Liq	Al2O3_Liq	FeOt_Liq	MnO_Liq	MgO_Liq	...	Di_Opx	Mgno_OPX	ln_Fm2Si2O6_liq	ln_FmAl2SiO6_liq	Kd_Fe_Mg_Fet	Kd_Fe_Mg_Fe2	Ideal_Kd	Delta_Kd_Fe_Mg_Fe2	Mgno_Liq_noFe3	Mgno_Liq_Fe2
0	51.1	-0.440763	0.251582	0.251582	Y	0.93	17.5	8.91	0.18	6.09	...	0.028142	0.828850	5.211708	-2.879647	0.251582	0.251582	0.304877	0.053295	0.549218	0.549218
1	51.5	7.599754	0.165104	0.165104	N	1.19	19.2	8.70	0.19	4.98	...	0.068126	0.860725	5.202722	3.931199	0.165104	0.165104	0.303256	0.138151	0.505036	0.505036
2	59.1	5.020447	0.187634	0.187634	N	0.54	19.1	5.22	0.19	3.25	...	0.074962	0.855382	5.851735	4.175071	0.187634	0.187634	0.277184	0.089550	0.526025	0.526025
3	52.5	0.947792	0.211297	0.211297	N	0.98	19.2	8.04	0.20	4.99	...	0.053125	0.839637	5.426741	1.519044	0.211297	0.211297	0.300632	0.089335	0.525239	0.525239
4	56.2	1.102032	0.144506	0.144506	N	0.34	20.4	5.88	0.20	2.58	...	0.033103	0.844054	6.297377	2.489832	0.144506	0.144506	0.290284	0.145777	0.438875	0.438875

5 rows × 92 columns

2c - Can overwrite input Fe3Fet_Liq ratio (or 0 if didnt enter one) with an integer

The affects delta Kd which only uses Fe2+ in the melt
you can compare the equilibrium tests from Fet and Fe2 in the output columns. For the equilibrium test, we only use Fe2+

[13]:

Temp_P29a_0H2O_30Fe=pt.calculate_opx_liq_press(opx_comps=Opxs, liq_comps=Liqs,
                                               equationP="P_Put2008_eq29a", T=1300, H2O_Liq=0,
                                               eq_tests=True, Fe3Fet_Liq=0.3)
Temp_P29a_0H2O_30Fe

[13]:

	SiO2_Liq	P_kbar_calc	eq_tests_Kd_Fe_Mg_Fet	eq_tests_Kd_Fe_Mg_Fe2	Kd Eq (Put2008+-0.06)	TiO2_Liq	Al2O3_Liq	FeOt_Liq	MnO_Liq	MgO_Liq	...	Di_Opx	Mgno_OPX	ln_Fm2Si2O6_liq	ln_FmAl2SiO6_liq	Kd_Fe_Mg_Fet	Kd_Fe_Mg_Fe2	Ideal_Kd	Delta_Kd_Fe_Mg_Fe2	Mgno_Liq_noFe3	Mgno_Liq_Fe2
0	51.1	-0.440763	0.251582	0.359403	Y	0.93	17.5	8.91	0.18	6.09	...	0.028142	0.828850	5.211708	-2.879647	0.251582	0.359403	0.304877	0.054526	0.549218	0.635106
1	51.5	7.599754	0.165104	0.235863	N	1.19	19.2	8.70	0.19	4.98	...	0.068126	0.860725	5.202722	3.931199	0.165104	0.235863	0.303256	0.067392	0.505036	0.593105
2	59.1	5.020447	0.187634	0.268049	Y	0.54	19.1	5.22	0.19	3.25	...	0.074962	0.855382	5.851735	4.175071	0.187634	0.268049	0.277184	0.009135	0.526025	0.613220
3	52.5	0.947792	0.211297	0.301853	Y	0.98	19.2	8.04	0.20	4.99	...	0.053125	0.839637	5.426741	1.519044	0.211297	0.301853	0.300632	0.001221	0.525239	0.612473
4	56.2	1.102032	0.144506	0.206437	N	0.34	20.4	5.88	0.20	2.58	...	0.033103	0.844054	6.297377	2.489832	0.144506	0.206437	0.290284	0.083846	0.438875	0.527708

5 rows × 92 columns

Example 3 - Iterating pressure and temperature

In reality, unles you are an experimentalist, you rarely know pressure and temperature
In Keith Putirka’s spreadsheets, you can link up columns to iterate P and T towards a solution, this can be done here using the function calculate_opx_liq_press_temp

3a - Iterating equation 29b from Putirka (2008) for P, and Beattie (1993) for temperature

Without specifying anything else, you get a dataframe with columns for calculated pressure and temperature

[14]:

PT_iter_29b_Beatt=pt.calculate_opx_liq_press_temp(opx_comps=Opxs, liq_comps=Liqs,
                                                  equationP="P_Put2008_eq29b",
                                                  equationT="T_Beatt1993_opx")
PT_iter_29b_Beatt

[14]:

	P_kbar_calc	T_K_calc
0	-2.083363	1396.863533
1	15.124832	1499.003345
2	15.723512	1496.583095
3	6.616612	1445.263817
4	6.404897	1400.627400

3b - As above, but specifying eq_tests=True

This returns equilibrium tests, you can check if they passed looking at the “Kd Eq (Put2008+-0.06)” column

[16]:

PT_iter_29b_Beatt_EqTests=pt.calculate_opx_liq_press_temp(opx_comps=Opxs, liq_comps=Liqs,
                       equationP="P_Put2008_eq29b", equationT="T_Beatt1993_opx", eq_tests=True)
PT_iter_29b_Beatt_EqTests

[16]:

	P_kbar_calc	T_K_calc	SiO2_Liq	eq_tests_Kd_Fe_Mg_Fet	eq_tests_Kd_Fe_Mg_Fe2	Kd Eq (Put2008+-0.06)	TiO2_Liq	Al2O3_Liq	FeOt_Liq	MnO_Liq	...	Di_Opx	Mgno_OPX	ln_Fm2Si2O6_liq	ln_FmAl2SiO6_liq	Kd_Fe_Mg_Fet	Kd_Fe_Mg_Fe2	Ideal_Kd	Delta_Kd_Fe_Mg_Fe2	Mgno_Liq_noFe3	Mgno_Liq_Fe2
0	-2.083363	1396.863533	51.1	0.251582	0.251582	Y	0.93	17.5	8.91	0.18	...	0.028142	0.828850	5.211708	-2.879647	0.251582	0.251582	0.304877	0.053295	0.549218	0.549218
1	15.124832	1499.003345	51.5	0.165104	0.165104	N	1.19	19.2	8.70	0.19	...	0.068126	0.860725	5.202722	3.931199	0.165104	0.165104	0.303256	0.138151	0.505036	0.505036
2	15.723512	1496.583095	59.1	0.187634	0.187634	N	0.54	19.1	5.22	0.19	...	0.074962	0.855382	5.851735	4.175071	0.187634	0.187634	0.277184	0.089550	0.526025	0.526025
3	6.616612	1445.263817	52.5	0.211297	0.211297	N	0.98	19.2	8.04	0.20	...	0.053125	0.839637	5.426741	1.519044	0.211297	0.211297	0.300632	0.089335	0.525239	0.525239
4	6.404897	1400.627400	56.2	0.144506	0.144506	N	0.34	20.4	5.88	0.20	...	0.033103	0.844054	6.297377	2.489832	0.144506	0.144506	0.290284	0.145777	0.438875	0.438875

5 rows × 93 columns

Example 4: Orthopyroxene only barometry

very similar to opx-liq functions, just dont need to specify liquid compositions
Most common problem is that equation 29c uses the ln of the Cr2O3 component, which if you dont enter any Cr, means the function returns a NaN (as you can’t ln a zero).

[17]:

Press=pt.calculate_opx_only_press(opx_comps=Opxs, equationP="P_Put2008_eq29c", T=1300)
Press

c:\users\penny\onedrive - oregon state university\postdoc\pymme\mybarometers\thermobar_outer\src\Thermobar\orthopyroxene_thermobarometry.py:209: UserWarning: The selected barometer uses the log of Cr2O3 component of Opx, which is zero for some of your compositions. This means the function will return infinity.
  w.warn('The selected barometer uses the log of Cr2O3 component of '
C:\Users\penny\anaconda3\lib\site-packages\pandas\core\arraylike.py:364: RuntimeWarning: divide by zero encountered in log
  result = getattr(ufunc, method)(*inputs, **kwargs)

[17]:

0    0.631893
1         NaN
2    5.410426
3    0.482388
4    0.397185
dtype: float64

Example 5: Plotting orthopyroxene compositions on a rhodes diagram

Option 1, specify simple=True, just uses 0.29 +-0.07 from Putirka (2008)
Option 2, specify a liquid composition (say lots of opxs from a single lava flow), calculates mean Si cation fraction for all liquids, uses this to calculate KD
Option 3, specify a min and max Kd

Step 1 - calculate Mg# for opx and liquid (can either treat FeT as Fe2, or partition into Fe2 and Fe3, only calculated Kd using Fe2)

[18]:

opx_comps_Fe3=pt.calculate_orthopyroxene_liquid_components(liq_comps=Liqs,
                                            opx_comps=Opxs, Fe3Fet_Liq=0.2)

Step 2 - calculate rhodes diagram lines between Mg#=0.4 and Mg#=0.7

This gives the simple values of Kd=0.29+0.06

[19]:

eq_lines_1=pt.calculate_opx_rhodes_diagram_lines(Min_Mgno=0.4, Max_Mgno=0.7)
eq_lines_1.head()

[19]:

	Mg#_Liq	Eq_Opx_Mg# (Kd=0.23)	Eq_Opx_Mg# (Kd=0.29)	Eq_Opx_Mg# (Kd=0.35)
0	0.400000	0.743494	0.696864	0.655738
1	0.403030	0.745892	0.699521	0.658579
2	0.406061	0.748269	0.702159	0.661402
3	0.409091	0.750626	0.704777	0.664207
4	0.412121	0.752962	0.707375	0.666994

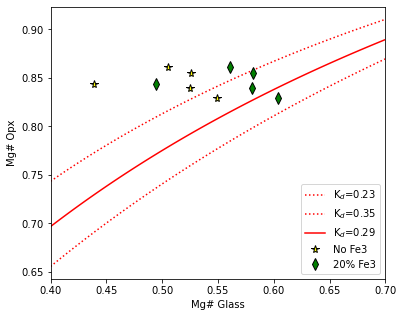
Step 3 - Plot these lines, along with measured opxs. Here we draw symbols where we account for Fe3+ (diamond), and just using Fet in the glas (stars)

[20]:

fig, (ax1) = plt.subplots(1, 1, figsize = (6,5))
ax1.plot(eq_lines_1['Mg#_Liq'], eq_lines_1['Eq_Opx_Mg# (Kd=0.23)'], ':r', label="K$_d$=0.23")
ax1.plot(eq_lines_1['Mg#_Liq'], eq_lines_1['Eq_Opx_Mg# (Kd=0.35)'], ':r', label="K$_d$=0.35")
ax1.plot(eq_lines_1['Mg#_Liq'], eq_lines_1['Eq_Opx_Mg# (Kd=0.29)'], '-r', label="K$_d$=0.29")
ax1.set_xlim([0.4, 0.7])
ax1.plot(opx_comps_Fe3['Mgno_Liq_noFe3'], opx_comps_Fe3['Mgno_OPX'], '*k', mfc='yellow', ms=8, label="No Fe3")
ax1.plot(opx_comps_Fe3['Mgno_Liq_Fe2'], opx_comps_Fe3['Mgno_OPX'], 'dk', mfc='green', ms=8, label="20% Fe3")
ax1.legend()
ax1.set_xlabel('Mg# Glass')
ax1.set_ylabel('Mg# Opx')

[20]:

Text(0, 0.5, 'Mg# Opx')

../../_images/Examples_Opx_and_Opx_Liq_Thermobarometry_Opx_Liq_Thermobarometry_39_1.png

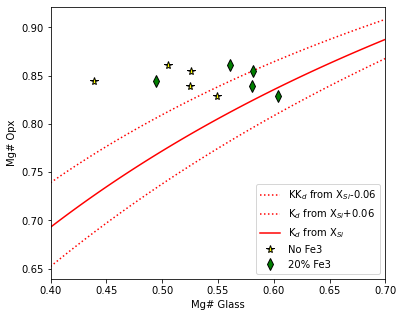
Example 5 - Rhodes diagram using a Kd model based on the Si content of the liquid

In this case, we enter a liquid composition into the rhodes diagram function
As this works by averaging the Si content of all inputted liquid to calculate Kd, this only recomended if liquids very similar in composition)

[21]:

eq_lines_2=pt.calculate_opx_rhodes_diagram_lines(Min_Mgno=0.4, Max_Mgno=0.7, liq_comps=Liqs)
eq_lines_2.head()

[21]:

	Mg#_Liq	Eq_Opx_Mg# (Kd=0.23)	Eq_Opx_Mg# (Kd=0.29)	Eq_Opx_Mg# (Kd=0.35)	Kd_XSi_P2008	Eq_Opx_Mg# (Kd_XSi_P2008)	Eq_Opx_Mg# (Kd_XSi_P2008)+0.06	Eq_Opx_Mg# (Kd_XSi_P2008)-0.06
0	0.400000	0.743494	0.696864	0.655738	0.295247	0.693063	0.652371	0.739169
1	0.403030	0.745892	0.699521	0.658579	0.295247	0.695739	0.655225	0.741593
2	0.406061	0.748269	0.702159	0.661402	0.295247	0.698396	0.658062	0.743997
3	0.409091	0.750626	0.704777	0.664207	0.295247	0.701033	0.660880	0.746380
4	0.412121	0.752962	0.707375	0.666994	0.295247	0.703650	0.663681	0.748743

[22]:

fig, (ax1) = plt.subplots(1, 1, figsize = (6,5))
ax1.plot(eq_lines_2['Mg#_Liq'], eq_lines_2['Eq_Opx_Mg# (Kd_XSi_P2008)-0.06'], ':r', label="KK$_d$ from X$_{Si}$-0.06")
ax1.plot(eq_lines_2['Mg#_Liq'], eq_lines_2['Eq_Opx_Mg# (Kd_XSi_P2008)+0.06'], ':r', label="K$_d$ from X$_{Si}$+0.06")
ax1.plot(eq_lines_2['Mg#_Liq'], eq_lines_2['Eq_Opx_Mg# (Kd_XSi_P2008)'], '-r', label="K$_d$ from X$_{Si}$")
ax1.set_xlim([0.4, 0.7])
ax1.plot(opx_comps_Fe3['Mgno_Liq_noFe3'], opx_comps_Fe3['Mgno_OPX'], '*k', mfc='yellow', ms=8, label="No Fe3")
ax1.plot(opx_comps_Fe3['Mgno_Liq_Fe2'], opx_comps_Fe3['Mgno_OPX'], 'dk', mfc='green', ms=8, label="20% Fe3")
ax1.legend()
ax1.set_xlabel('Mg# Glass')
ax1.set_ylabel('Mg# Opx')

[22]:

Text(0, 0.5, 'Mg# Opx')

../../_images/Examples_Opx_and_Opx_Liq_Thermobarometry_Opx_Liq_Thermobarometry_42_1.png